Matematik

Funktioner af to variable

08. maj 2021 af inneedofhomework - Niveau: A-niveau

Hej. Jeg synes, denne opgave (vedhæftet) er ret svær at løse...

Er der en, der kan hjælpe med at udregne denne opgave? Helst trinvist så jeg kan blive fortrolige med, hvordan man regner den.

Tak på forhånd!

Vedhæftet fil: Skærmbillede 2021-05-08 kl. 16.04.19.png

Brugbart svar (1)

Svar #1
08. maj 2021 af ringstedLC

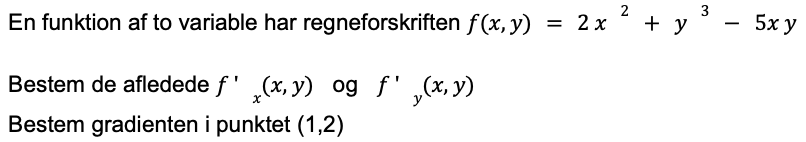
$\begin{align*} \frac{\partial }{\partial x}f(x,y)={f_x}'(x,y) &= \bigl(2x^2+k^3-5kx\bigr)' \\ \frac{\partial }{\partial y}f(x,y)={f_y}'(x,y) &= \bigl(...\bigr)' \end{align*}$

Se eventuelt https://www.webmatematik.dk/lektioner/matematik-a/funktioner-af-to-variable/partielle-afledede

Brugbart svar (1)

Svar #2
08. maj 2021 af ringstedLC

$\begin{align*} \nabla f(x,y) &= \left ( \frac{\partial }{\partial x},\frac{\partial }{\partial y} \right )f(x,y) \\ \nabla f(1,2) &= \left ( \frac{\partial }{\partial x},\frac{\partial }{\partial y} \right )f(1,2) \\ &= \Bigl ( {f_x}'(x,y)\cdot f(1,2)\,,{f_y}'(x,y)\cdot f(1,2) \Bigr )=\Bigl(?,?\Bigr) \end{align*}$

Se eventuelt https://www.webmatematik.dk/lektioner/matematik-a/funktioner-af-to-variable/gradient

Brugbart svar (0)

Svar #3
08. maj 2021 af AMelev

Se formelsamling side 33 (194) og (195)

#2 ??? Er gradienten ikke bare (f_x'(1,2), f_Y'(1,2))? Hvor kommer produktet (·f(1,2)) ind?

Brugbart svar (1)

Svar #4
09. maj 2021 af ringstedLC

#2 Rettelse:

$\begin{align*} \nabla f(x,y) &= \left ( \frac{\partial }{\partial x},\frac{\partial }{\partial y} \right )f(x,y) \\ \nabla f(1,2) &= \left ( \frac{\partial }{\partial x},\frac{\partial }{\partial y} \right )f(1,2) \\ &= \Bigl ( {f_x}'(1,2)\,,{f_y}'(1,2) \Bigr )=\Bigl(?,?\Bigr) \end{align*}$

... burde selv have set eksemplet i linket igennem.

Svar #5
18. maj 2021 af inneedofhomework

Jeg forstår ikke helt... hvad giver resultatet ud fra dine beregninger?

Brugbart svar (0)

Svar #6
18. maj 2021 af AMelev

Se #3 og formelsamling.

Svar #7
18. maj 2021 af inneedofhomework

Jeg forstår det ikke helt stadig...

Brugbart svar (0)

Svar #8
18. maj 2021 af AMelev

Har du fundet formlen (195) i din formelsamling?
Du ved jo, hvordan du bestemmer de partielle afledede, og så er det bare at beregne deres værdier i
(x,y) = (1,2) og sætte det ind i gradienten, som er en vektor.

Svar #9
18. maj 2021 af inneedofhomework

er det (2,2)?? Eller...?

Brugbart svar (0)

Svar #10
18. maj 2021 af AMelev

Du skal bestemme gradienten i (1,2) iflg. opgaven. Og nej, det er ikke $\binom{2}{2}$
Upload det, du har lavet.

Svar #11
18. maj 2021 af inneedofhomework

er det (14,11)?

Brugbart svar (0)

Svar #12
19. maj 2021 af AMelev

Læg et billede op af dine beregninger.

Skriv et svar til: Funktioner af to variable

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.