Matematik

cirkler

01. juni 2021 af Carolineshm - Niveau: B-niveau

Er der en som kan hjælpe med opgave 1c og sætte det ind for mig i formlen, da jeg ikke kan få det til at give mening.

Jeg har også brug for hjælp i opgave 1e

Vedhæftet fil: Skærmbillede 2021-06-01 kl. 02.38.26.png

Brugbart svar (0)

Svar #1
01. juni 2021 af PeterValberg

Jeg indsætter lige dit vedhæftede billede, det gør det nemmere at hjælpe

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

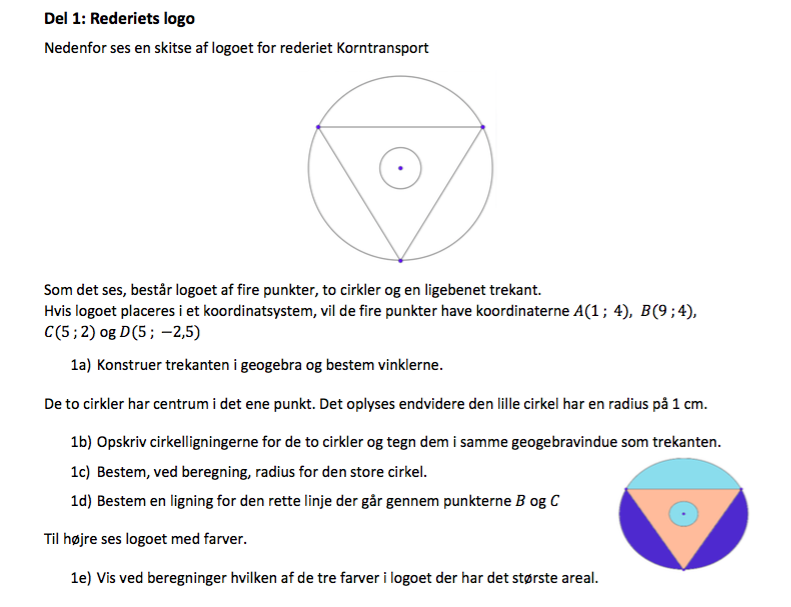
Svar #2
01. juni 2021 af PeterValberg

Arealet af den lyse trekant kan bestemmes vha. Herons formel,
hvis du benytter afstandsformlen til at bestemme længden af
siderne i trekanten, - husk at fratrække arealet af den lille cirkel.
Alternativt kan du bestemme trekantens areal vha. "Den halve appelsin" formel,
hvis du også har bestemt trekantens vinkler

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
01. juni 2021 af PeterValberg

For at bestemme arealet af de tre cirkelafsnit, kan du benytte
formlen herfor, som du kan se her: < LINK >

Til bestemmelse af (center)vinklen kan du udnytte, at du har bestemt
trekantens vinkler samt forholdet mellem center- og periferivinkler < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #4
01. juni 2021 af mathon

$\small \begin{array}{llllll}& A_{\textup{cirkelafsnit}}&\textup{n\aa r centervinklen m\aa les i \textbf{radianer}}\\\\&& A_{\textup{cirkelafsnit}}=\frac{1}{2}\cdot r^2\cdot \left ( v-\sin(v) \right )=\frac{1}{2}\cdot \left ( \sqrt{20} \right )^2\cdot \left ( \frac{2\pi}{3}-\sin\left ( \frac{2\pi}{3} \right ) \right )=\\\\&& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \! \! \! \! \frac{1}{2}\cdot 20\cdot \left ( \frac{2\pi}{3}-\frac{\sqrt{3}}{2} \right )=12.2837 \end{array}$

Brugbart svar (0)

Svar #5
01. juni 2021 af mathon

$\small \small \begin{array}{llllll}& A_{\textup{ligebenet trekant}}\qquad \textup{n\aa r siden kaldes }a\\\\& A_{\textup{ligebenet trekant}}=\frac{\sqrt{3}}{4}\cdot a^2 \end{array}$

Svar #6
01. juni 2021 af Carolineshm

Tak for hjælpen

Skriv et svar til: cirkler

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.