Matematik

Integration ved substitution

03. september 2021 af azulodukovic - Niveau: Universitet/Videregående

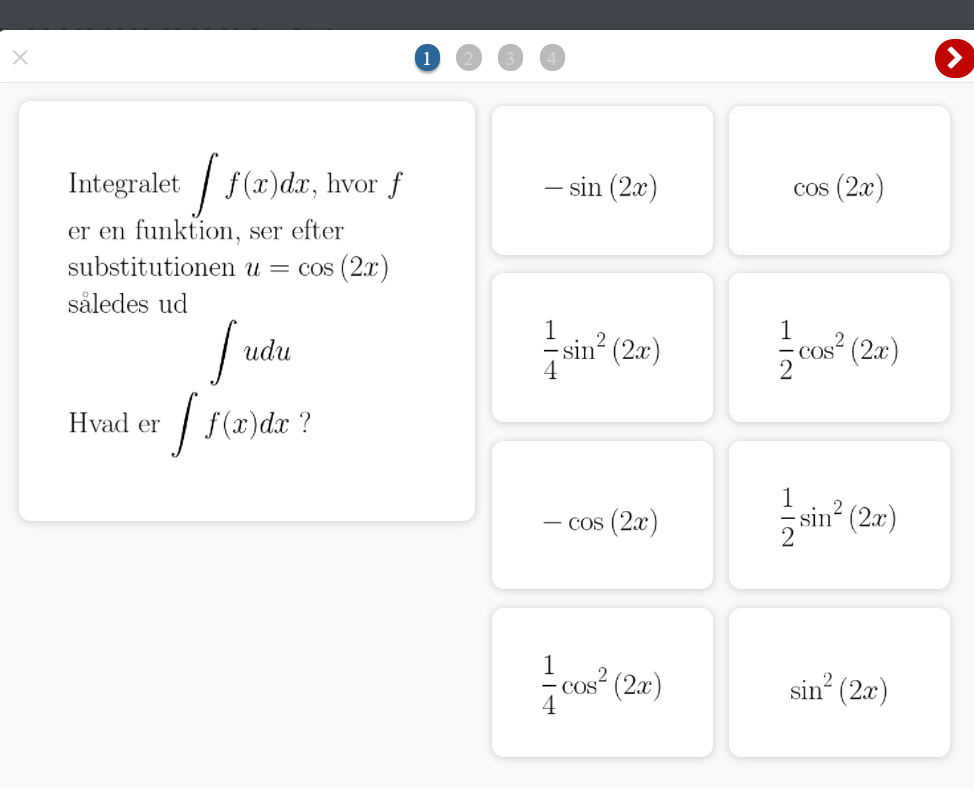
Nogen der kender fremgangsmåden og resultat til følgende. Svarmuligheder er til højre for spørgsmålet.

Vedhæftet fil: 241275857_982766972558361_8108817803407354691_n.png

Brugbart svar (0)

Svar #1
03. september 2021 af Soeffi

#0. Indsætter billede:

Lidt forvirrende, men:

$\int udu=\frac{1}{2}u^2=\frac{1}{2}cos^2(2x)$

Brugbart svar (0)

Svar #2
03. september 2021 af mathon

$\small \begin{array}{lllll} \textup{Ikke forvirrende:}\\& \int u\,\mathrm{d}u=\frac{1}{2}u^2\\\\ \textup{tilbagesubstitution}\\ \textup{giver:}\\& \frac{1}{2}\cdot \left (\cos(2x) \right )^2=\frac{1}{2}\cdot \cos^2(2x) \end{array}$

Brugbart svar (0)

Svar #3
03. september 2021 af Soeffi

#0. Bemærk at man ikke behøver at kende f(x) inden beregningen af det ubestemte integrale.

Skriv et svar til: Integration ved substitution

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.