Matematik

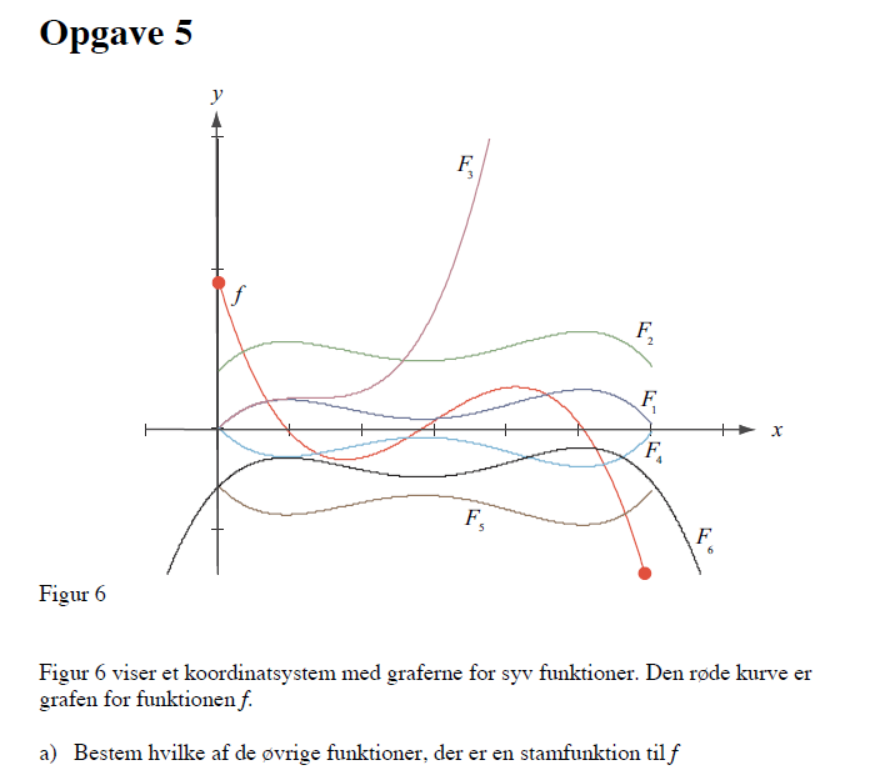
Bestem hvilke af de øvrige funktioner, der er stamfunktion til f

16. oktober 2021 af Alexzi - Niveau: A-niveau

Hej derude

Jeg sidder med enopgave som jeg har lidt svært ved. Hvordan er det nu funktionen f er i forhold til stamfunktionen? Det er noget med at når funktionen f har nulpunkt skal stamfunktionen have ekstrema, eller er jeg helt væk?

Ville være dejligt med en grundig forklaring og et evt svar, da jeg har lidt flere opgaver der minder meget om den her.

Vedhæftet fil: Eksamensopgave 2010 (1).PNG

Brugbart svar (0)

Svar #1
16. oktober 2021 af peter lind

Brugbart svar (1)

Svar #2
16. oktober 2021 af peter lind

Når den f >0 er dens stamfunktion voksende. Det er den for x<1

Når den f < 0 er dens stamfunktion aftagende

Du gennemgår bare funktionerne systematisk og sletter dem der ikke passer til det

Svar #3
16. oktober 2021 af Alexzi

Hvis vi bare kigger på det første stykke, er det så rigtigt at vi kan fjerne f4, f5 og f6, da deres stamfunktion ikke er voksende når x er mindre end 1?

Svar #4
16. oktober 2021 af Alexzi

Mit bud på opgaven ville være at f1 og f2 er det rigtige svar. Ret mig lige med forklaring hvis ikke

Brugbart svar (1)

Svar #5
16. oktober 2021 af ringstedLC

#4: Det er korrekt.

$\begin{align*} F(x)=\int \!f(x)\,\mathrm{d}x &\Rightarrow f(x)=F'(x)\quad \textup{(definition)} \\ {F_1}'(x) &\geq 0\,,\;0\leq x\leq 1 \\ \Rightarrow f(x) &\geq 0 \\ {F_1}'(x) &\leq 0\,,\;1\leq x\leq 3 \\ \Rightarrow f(x) &\leq 0 \\\\ \textup{Bem\ae rk: }F_2(x)=F_1(x)+k &\Rightarrow {F_2}'(x)={F_1}'(x) \end{align*}$

Svar #6
16. oktober 2021 af Alexzi

Super fedt tak for det ringstedLC :)

Nu hvor du virker så kvik, er det så samme løsningsmodel til denne som opgaven ovenover eller er det en anden metode man skal have fat i?

Vedhæftet fil:eksamen 2019 STX (1).PNG

Brugbart svar (1)

Svar #7
16. oktober 2021 af peter lind

ja det er det

Skriv et svar til: Bestem hvilke af de øvrige funktioner, der er stamfunktion til f

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.