Matematik

Ligevægt kræfter

16. oktober 2021 af DeepOcean - Niveau: B-niveau

Hej Alle . Har brug for lidt hjælp for følgende opgave .

Vi har et hjul diameter svar til 520 mm . Hjulet er drejet således at de 6 hjul-eger peger som vist på vedlagt figur .

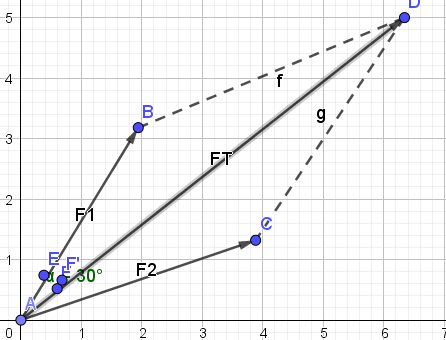
For hjulet gælder, at tyngdekraften, FT, er i ligevægt med kræfterne F1 og F2 og har samme retning som to af hjul-egerne.

At kræfterne er i ligevægt betyder $\underset{F1}{\rightarrow} +\underset{F2}{\rightarrow} +\underset{FT}{\rightarrow} =\binom{0}{0}$
Vi kender størrelse $\underset{FT}{\rightarrow}$ = 1487

Bestem længde af $\underset{F1}{\rightarrow}$ og $\underset{F2}{\rightarrow}$ ?

Vedhæftet fil: ligevægt kræfter.PNG

Brugbart svar (0)

Svar #1
16. oktober 2021 af peter lind

Der mangler en oplysning. Kom med hele opgaven

Brugbart svar (0)

Svar #2
16. oktober 2021 af jantand

Vinklen mellem F1 og F2 er 60 grader.

Dvs. viklen til lodret er 30 grader for F1 of det samme for F2.

Så kan du regne ud hvor store F1 og F2 er da de er modsat rettet FT altså - 1487 husk at regne de 30 grader ind i ligningen . F1 og F2 er lige store.

Svar #3
16. oktober 2021 af DeepOcean

#2 Jeg er klar over at vinklen mellem F1 og F2 er 60 grader men hvordan kan vi beregne størrelse af F1 og F2 ? har du nogle ide ..?

Brugbart svar (0)

Svar #4
16. oktober 2021 af jantand

Vinklen mellem lodret og F1 er 30 grader. Ligeså med F2.

Så du har kræfternes parallelogram.

Så kan du regne kræfterne ud.

Svar #5
16. oktober 2021 af DeepOcean

#4 Jeg har regnet F1 med at bruge parallelogram til 858.51 ..Jeg ved at F1+F2 = 1487 => F2 = 1487-858.51 = 628.49

Har brugt $\frac{F1}{Sin(30)}=\frac{1487}{Sin(120)}=> F1=858.51$

Men når jeg bruger samme metode ( Parallelogram) så får jeg F2 til 858.51 og F1 til 628.49 ..!

er der sådan skal forståes at F1 og F2 kan har to værdier alt efter hvad man har starte med at beregne ?

Brugbart svar (0)

Svar #6
16. oktober 2021 af peter lind

nej F1cos(0)+F2cos(30) = FT og F1=F2

Svar #7
16. oktober 2021 af DeepOcean

Har du konkludere at F1= F2 ud fra figur..?

Hvordan har du betragte vinklen 0 og dermed F1Cos(0)?

Svar #8
16. oktober 2021 af DeepOcean

Jeg har tegne Parallelogram....med 30 grad ,,så hvordan har du fundet 0 grad

Vedhæftet fil:Parallelogram.PNG

Brugbart svar (0)

Svar #9
16. oktober 2021 af peter lind

Brugbart svar (0)

Svar #10
16. oktober 2021 af peter lind

den er forkert tegnet

FT er lodret vinklen mellem kræfterne og lodret er 30º grader. Projektionen ind på lodret er så F*cos(30)

Brugbart svar (1)

Svar #11
16. oktober 2021 af ringstedLC

$\begin{align*} \left |\overrightarrow{F_t} \right |=1487\,(\textup{N}) \Rightarrow \overrightarrow{F_t} &= \binom{0}{-1487} \\ \overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_t} &= \binom{0}{0} \\ \overrightarrow{F_1}+\overrightarrow{F_2}=-\overrightarrow{F_t} &= \binom{0}{1487} \\ \binom{\cos(120^{\circ})}{\sin(120^{\circ})}\cdot \left |\overrightarrow{F_1}\right | +\binom{\cos(60^{\circ})}{\sin(60^{\circ})}\cdot \left |\overrightarrow{F_2}\right | &= \binom{0}{1487} \\ \binom{0}{2\sin(60^{\circ})}\cdot \left |\overrightarrow{F_1}\right | &= \binom{0}{1487} \;,\;\left |\overrightarrow{F_1}\right |=\left |\overrightarrow{F_2}\right | \\ \left |\overrightarrow{F_1}\right | &= \frac{1487}{2\sin(60^{\circ})}=\;?\,(\textup{N}) \end{align*}$

Svar #12
16. oktober 2021 af DeepOcean

#11

så F1 er 858.51 N ..Da F1 = F2 så F2 = 858.51 N ...Men i følge opgaven F1 +F2 = 1487 og i følge beregninger 858.51 + 858.51 = 1717.03 og ikke 1487 !! så Er der en fejl i jeres beregninger ?

Brugbart svar (1)

Svar #13
16. oktober 2021 af ringstedLC

#12:

$\begin{align*} \textup{L\ae ngde\,af}\;\overrightarrow{F_1}=\left |\overrightarrow{F_1} \right |=F_1 &= 851.52\;(\textup{N}) \\ \overrightarrow{F_1} &= 851.52\cdot \!\binom{\cos(120^{\circ})}{\sin(120^{\circ})} \\ \overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_t}=\overrightarrow{0} &\underset{\textup{medf\o rer\,ikke\,at}}{\nRightarrow} \left |\overrightarrow{F_1} \right |+\left |\overrightarrow{F_2} \right | +\left |\overrightarrow{F_t} \right |=\left | \overrightarrow{0} \right |=0 \\ &\underset{\textup{medf\o rer\,ikke\,at}}{\nRightarrow}F_1+F_2+F_t=0 \end{align*}$

Brugbart svar (1)

Svar #14
16. oktober 2021 af ringstedLC

#13 supplerende:

$\begin{align*} \overrightarrow{F_1} &= \left | \overrightarrow{F_1} \right | \cdot \binom{\cos(120^{\circ})}{\sin(120^{\circ})} \\ \binom{\cos(120^{\circ})}{\sin(120^{\circ})} &= \frac{\overrightarrow{F_1}}{\left | \overrightarrow{F_1} \right |} \\ \vec{e}_{\overrightarrow{F_1}} &= \frac{\overrightarrow{F_1}}{\left | \overrightarrow{F_1} \right |} \quad \textup{formel (43, (44) og (45)} \\ \left | \vec{e\,} \right | &= 1\;,\;\sin(v)^2+\cos(v)^2=1^2\end{align*}$

Brugbart svar (0)

Svar #15
16. oktober 2021 af jantand

F1*cos(30)+F2*cos(30)=1487

Da F1=F2 så er F1*cos(30) =743,5

F1= 743,5/Cos(30)=834,44956

Jeg tror du er nødt til at begynde forfra på kræfternes parallelogram og sinusreletioner.

Inden du løser en opgave skal du tegne den først.

Hvordan har du fået tegningen til at ligge på skrå. Den orindelige kraft er lodret

Svar #16
16. oktober 2021 af DeepOcean

#11 , #13 , #14 Tak for det. Med din hjælp har jeg forstået opgave .1000 tak

Svar #17
16. oktober 2021 af DeepOcean

#15 Tak for dit forslag..

Skriv et svar til: Ligevægt kræfter

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.