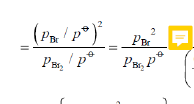Matematik

Hvordan får jeg et udtryk med gange når der står dividere

13. januar 2022 af Amalie1234324 - Niveau: A-niveau

Hejsa,

Ved i hvordan man ender med udtrykket til højre. Forstår ikke hvordan gange opnås i nævneren.

Fortsæt en god dag :)

Vedhæftet fil: how to go.PNG

Brugbart svar (0)

Svar #1
13. januar 2022 af peter lind

Brugbart svar (0)

Svar #2
13. januar 2022 af peter lind

Man dividerer med en brøk ved at gange med den omvendte altså 1/(a/b) = b/a

Svar #3
14. januar 2022 af Amalie1234324

Kan du vise det med en udførsel? Det vil betyde en del :)

Brugbart svar (0)

Svar #4
14. januar 2022 af OliverHviid

Se vedhæftede:

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #5
14. januar 2022 af probabilist

Det vil nok være til nytte for dig at huske, at for reelle tal a og b, der er forskellige fra 0, så er division defineret som a ganget med den mulitplikative inverse til b. Hvis b^-1 er den multiplikativt inverse til b, så betyder det altså, at

$\forall a,b \in \mathbb{R} \setminus \{0\}\ : \frac{a}{b}:=a\cdot b^{-1}$ .

Så hvis du vil vise Peters sætning for a,b i R\{0}, så er

$\frac{1}{(\frac{a}{b})}=1\cdot (\frac{a}{b})^{-1}=\frac{b}{a},$

hvor vi bruger, at (b/a) er den multiplikativt inverse af (a/b), hvilket er indlysende, da

$\frac{a}{b}\cdot \frac{b}{a}=1$ .

Du arbejder med

$\frac{(p_a/p^b)^2}{p_c/p^b}=\frac{(p_a^2/p^{2b})}{p_c/p^b}=\frac{p_a^2\cdot p^{-2b}}{p_c \cdot p^{-b}} =\frac{p_a^2}{p_c \cdot p^{-b} \cdot p^{2b}}= \frac{p_a^2}{p_c \cdot p^{2b-b}}=\frac{p_a^2}{p_c \cdot p^{b}}$ .

Her har vi kun brugt definition på division samt at (a b)^n=a^n b^n og a^m a^n= a^(m+n).

Skriv et svar til: Hvordan får jeg et udtryk med gange når der står dividere

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.