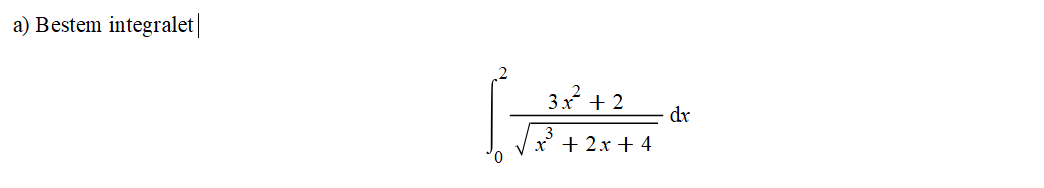Matematik

Bestem intregalet

08. februar 2022 af Mariassssssss - Niveau: A-niveau

HEJ SP

Jeg har brug for hjælp til vedhæftede opgave (DEN ER UDEN HJÆLPEAMIELER).

Gerne med forklaring/formler:)

På forhånd tak

Vedhæftet fil: integral.PNG

Brugbart svar (0)

Svar #1
08. februar 2022 af mathon

Svar #2
08. februar 2022 af Mariassssssss

Kan du hjælpe Mathon?

Brugbart svar (0)

Svar #3
08. februar 2022 af mathon

$\small \begin{array}{llllll} \textup{s\ae t }\\& u=x^3+2x+4\quad \textup{og dermed }\quad \mathrm{d}u=(3x^2+2)\mathrm{d}x\quad \int_{0}^{2}...\mathrm{d}x\rightarrow \int_{4}^{16}...\mathrm{d}u \end{array}$

Brugbart svar (0)

Svar #4
08. februar 2022 af mathon

$\small \small \begin{array}{llllll} \int_{0}^{2}\frac{3x^2+2}{\sqrt{x^3+2x+4}}\mathrm{d}x=\int_{0}^{2}\frac{1}{\sqrt{x^3+2x+4}}\cdot \left ( 3x^2+2 \right )\mathrm{d}x=\int_{4}^{16}\frac{1}{\sqrt{u}}\, \mathrm{d}u\\\\ x\neq -1.17951 \end{array}$

Svar #5
08. februar 2022 af Mariassssssss

Hvad mener du med "du" mener du "dx"?

Brugbart svar (0)

Svar #6
08. februar 2022 af mathon

$\small \small \small \small \small \begin{array}{llllll}\\\\ \textup{for }x\neq-1.17951\\\\ \int_{0}^{2}\frac{3x^2+2}{\sqrt{x^3+2x+4}}\mathrm{d}x=\int_{0}^{2}\frac{1}{\sqrt{x^3+2x+4}}\cdot \left ( 3x^2+2 \right )\mathrm{d}x=\int_{4}^{16}\frac{1}{\sqrt{u}}\, \mathrm{d}u=\\\\ 2\cdot \int_{4}^{16}\frac{1}{2\sqrt{u}}\, \mathrm{d}u=2\cdot \left [ \sqrt{u} \right ]_{4}^{16}=2\cdot \left ( \sqrt{16}-\sqrt{4} \right )=2\cdot (4-2)=2\cdot 2=4 \end{array}$

Svar #7
08. februar 2022 af Mariassssssss

Jeg skal ikke finde løsningen blot bestemme integralet..

Svar #8
08. februar 2022 af Mariassssssss

Hov jeg forstår nu, men ved stadig ikke havd du mener med U???

Brugbart svar (0)

Svar #9
08. februar 2022 af mathon

... enten du bruger t eller u for den variable er blot en vanesag.
t har det med uagtsomt "at forsvinde" som et 1-tal i sammenskrivning med cifre, hvorfor jeg vælger u .

Brugbart svar (0)

Svar #10
08. februar 2022 af mathon

u er den substituerede, bekvemmere funktion til brug ved substitutionen.

Svar #11
08. februar 2022 af Mariassssssss

argg tak for hjælpen !

Brugbart svar (0)

Svar #12
08. februar 2022 af AMelev

#5 Hvis x er den uafhængige variabel, der skal integres med hensyn til, angives det i integralet med dx.
Tilsvarende angives det med du, hvis den uafhængige variabel hedder u.
Fx kan funktionen y = x²·u betragtes enten som en funktion af x eller en funktion af u.
Hvis x er den uafhængige variabel, er u at betragte som en konstant, og så fås $\int y\, dx=\int x^2\cdot u \, dx=u\cdot \int x^2\, dx=u\cdot \frac{1}{3}x^3+k$

og tilsvarende med u som uafhængig variabel (x konstant) fås $\int y\, du=\int x^2\cdot u\, du=x^2\cdot \int u\, du=x^2\cdot \frac{1}{2}u^2 +k$

En kendt "snydeopgave" er $\int 2x\, dt$

$\int 2x\, dt=2x\cdot t +k$ ikke, som mange lader sig forlede til at skrive, $x^2+k$

Skriv et svar til: Bestem intregalet

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.