Matematik

Skæring af plan og punkt

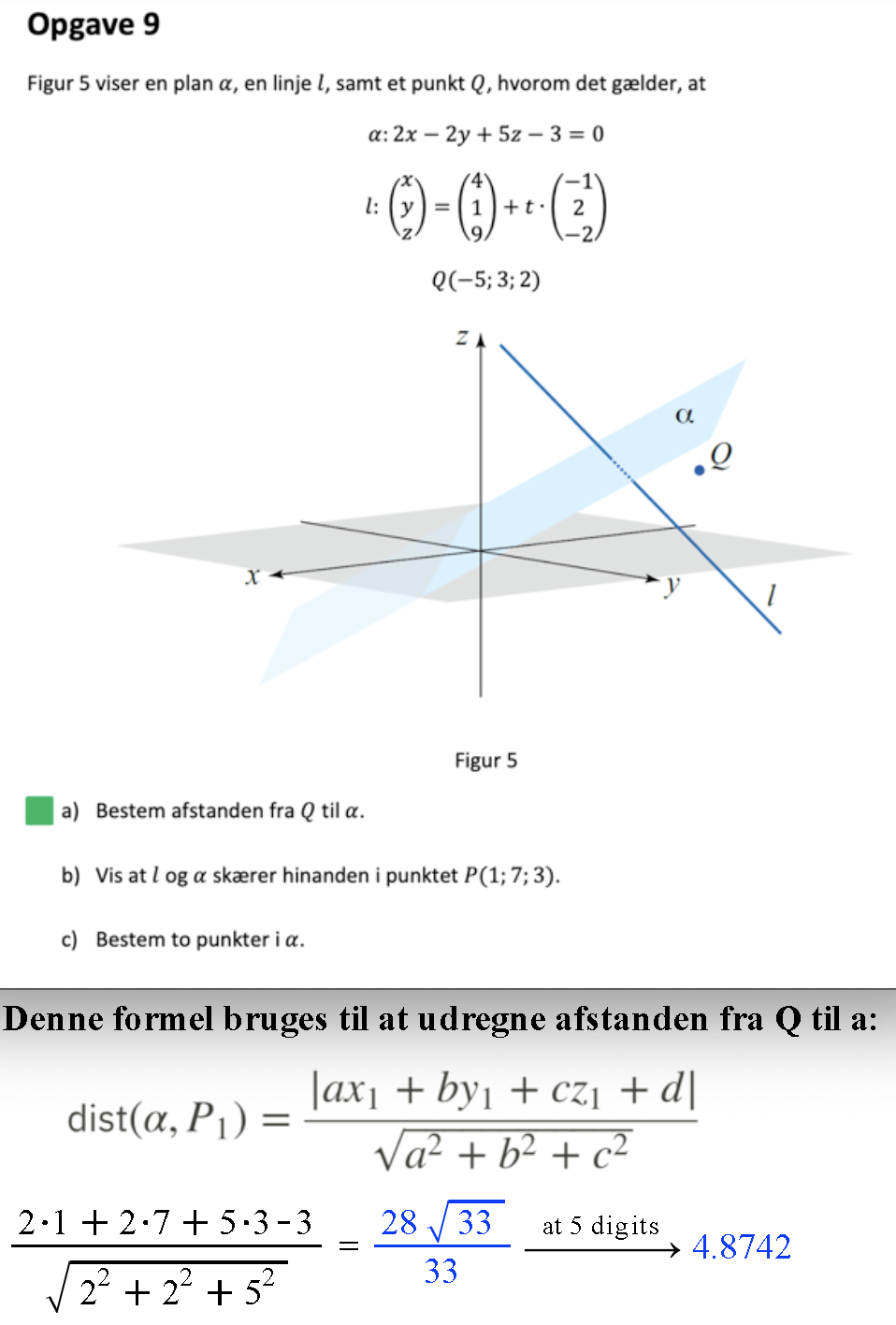
11. februar 2022 af Arbejdshesten - Niveau: A-niveau

Formlen der ses på det vedhæftet billede er ret forvirrende.

Jeg har sat værdierne ind som burde være korrekt, men i det eksempel jeg så, blev der f.eks. minusset pga. negativ b-værdi istedet for at plusse, som formlen siger man skal øverst i brøkken . Men da jeg indsat minus i et af stederne, gav det 0, hvilket ikke kan være rigtigt.

Derfor vil jeg gerne have hjælp til, hvordan den rigtigt skrives op, og om det faktisk er den formel der skal bruges.

Vedhæftet fil: Skærmbillede 2022-02-11 kl. 17.17.20.png

Brugbart svar (0)

Svar #1
11. februar 2022 af peter lind

Brugbart svar (0)

Svar #2
11. februar 2022 af peter lind

Du skal bruge minus når der står minus og det bliver ikke 0. Tælleren bliver

2*(-5) -2*3 + 2*5 -3

Svar #3
11. februar 2022 af Arbejdshesten

okay, men er det gange imellem (-5) -2 som du har skrevet? samt ved 2*5 -3, altså gange mellem 5 og -3? og skal der ikke stå parantes mellem -2 og -3?

Svar #4
11. februar 2022 af Arbejdshesten

Har prøvet sådan her, men tror næppe det er korrekt:

Svar #5
11. februar 2022 af Arbejdshesten

Her:

Vedhæftet fil:Skærmbillede 2022-02-11 kl. 18.01.44.png

Svar #6
11. februar 2022 af Arbejdshesten

Brugbart svar (0)

Svar #7
11. februar 2022 af peter lind

Der står 2x sætter -1 ind for x får du 2(-5) = -10 Den næster står der -2x og der skal du så sætte 3 ind for x.

Det er simpel regning og det burde have lært for længst

Svar #8
11. februar 2022 af Arbejdshesten

Ja, men selvom værdierne er sat ind korrekt, får man et forvirrende svar:

Vedhæftet fil:Skærmbillede 2022-02-11 kl. 20.02.17.png

Brugbart svar (1)

Svar #9
11. februar 2022 af ringstedLC

a) Du indsætter forkert og negligerer at tage den numeriske værdi.

$\begin{align*} \textup{dist}(\alpha ,Q) &= \frac{\left |a\,x_Q+b\,y_Q+x\,z_Q+d \right |}{\sqrt{a^2+b^2+c^2}} \\ &= \frac{\left |2\cdot (-5)-2\cdot 3+5\cdot 2-3 \right |}{\sqrt{2^2+(-2)^2+5^2}} \\ \textup{dist}(\alpha ,Q) &= \frac{9}{\sqrt{33}}\approx 1.57 \end{align*}$

Brugbart svar (0)

Svar #10
11. februar 2022 af OliverHviid

#8 Husk nu at tælleren er den numeriske værdi.

Svar #11
11. februar 2022 af Arbejdshesten

Altså skal jeg have de 2 lodrette streger, korrekt?

Brugbart svar (0)

Svar #12
11. februar 2022 af ringstedLC

Nævneren kan kun blive positiv, så for at afstand/distance bliver positiv i afstands- og distanceformler, hvor normalvektoren benyttes, er det altid den numeriske værdi.

$\begin{align*} \alpha :2x-2y+5z-3 &= 0\Rightarrow \vec{\,n}_1 =\begin{pmatrix} 2\\-2\\5 \end{pmatrix} \\ \alpha :-2x+2y-5z+3 &= 0\Rightarrow \vec{\,n}_2 =\begin{pmatrix} -2\\2\\-5 \end{pmatrix}=-1\cdot \begin{pmatrix}2\\-2\\ 5\end{pmatrix} \\ \frac{2\cdot (-5)-2\cdot 3+5\cdot 2-3}{\sqrt{33}} &\;{\color{Red} \neq }\;\frac{-2\cdot (-5)+2\cdot 3-5\cdot 2+3}{\sqrt{33}} \\ \frac{\left |2\cdot (-5)-2\cdot 3+5\cdot 2-3 \right |}{\sqrt{33}} &= \frac{\left |-2\cdot (-5)+2\cdot 3-5\cdot 2+3 \right |}{\sqrt{33}} \\ \end{align*}$

Svar #13
11. februar 2022 af Arbejdshesten

Forstået, men måden man gør det på CAS, er bare at lave de lodrette streger på hver ende?

Brugbart svar (0)

Svar #14
11. februar 2022 af ringstedLC

Ærlig talt; det er på høje tid, at du selv finder ud af, hvordan du bruger den slags relativt simple kommandoer i din CAS. Læs manualen, søg på nettet eller test selv dit forslag.

Svar #15
11. februar 2022 af Arbejdshesten

Jeg vil bare gerne vide, om det er de lodrette streger der gør forskellen i formlen, eller finder den numeriske værdi. Og er 1,57 det rigtige svar?

Brugbart svar (1)

Svar #16
11. februar 2022 af OliverHviid

De "lodrette streger" betyder at der er tale om den numeriske værdi - og ja, 1,57 er korrekt.

Svar #17
11. februar 2022 af Arbejdshesten

Det er modtaget :)

Brugbart svar (1)

Svar #18
11. februar 2022 af SuneChr

Ang. afstandsformlen, normalvektor og numerisktegn:
Afstande regner vi normalt positive, derfor er der numerisktegn.
Afstanden punkt/plan er positiv, når punktet ligger i rummet planens normalvektor peger ind i.
Afstanden punkt/plan er negativ, når punktet ligger i rummet planens normalvektor peger væk fra,
af den grund sætter vi numerisktegnet.

Svar #19
11. februar 2022 af Arbejdshesten

I see, men jeg ved, at de lodrette streger kendetegner afstand, og har i nogle opgaver derfor brugt afstandsformlen mellem de lodrette streger.
Så det er ikke i alle tilfælde, ligesom her, at man bruger afstandsformlen, bare fordi der er de lodrette streger?

I så fald, hvordan skal man så vide, om det er afstandsformlen eller numeriske værdier man skal bruge?

Brugbart svar (0)

Svar #20
11. februar 2022 af peter lind

Man bruger de lodrette streger fordi afstande regnes positivne. Man kan godt bruge de lodrette streger selvom det ikke er afstandsformlen

Forrige 1 2 Næste

Der er 23 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.