Undersøge asymptote, Opgave 811

Det betyder at x+1 er faktor i både tæller og nævner og den kan du forkorte ud

#0. Graf i Geogebra.

#0. Hvis a er rod i både tæller og nævner, så vil der være lodret asymptote for x = a, hvis a's multiplicitet er højere i nævnerpolynomiet end i tællerpolynomiet. 

Tak for svaret

Jeg ser på det.

 #3 Det er ikke sikkerrt. Der kan være dobbelt rod tælleren

y = ax² + bx + c opløses i faktorer  a • ( x - a ) • ( x - b )

jeg indsætter så rødderne fra tælleren x₁ = -1 , x₂ = 2 og roden x = -1 fra nævneren i ovenstående og omskriver funtkionen f

                x²  - x - 2               ( ( x - ( -1 ))  • ( x - 2 )                ( x + 1 ) • ( x - 2 )               x - 2

f ( x ) = ------------------- =  --------------------------------------  = ------------------------------- =  -------------- 

               x² + 2x + 1           ( ( x - ( - 1 ))• (( x - ( -1 ))               ( x + 1 ) • ( x + 1 )             x + 1

Grafen må have et hul hvis x = -1 så bliver nævneren 0,så tallet må jo nærme sig  x = -1 så hvis man omskriver tælleren med  -1 og nævner med -1 og dividere med  x i tæller og nævner

                                                     - ( - x + 2 )                          2

                                                   -------------------             1 +  -----

    x - 2            - ( -x + 2 )                      x                                  x 

------------  =  ------------------- =  -----------------------  =   ------------------   = -1    når x → ∞  får jeg  

   x  + 1            - ( x - 1 )                 - ( x + 1 )                          - 1

                                                   ---------------------            -1   -------

                                                            x                                    x

                   x²  - x - 2               

lim          ---------------------    = -  1    så har grafen en lodret asymptote i x = -1        

x → ∞         x² + 2x + 1             

Mit spørgsmål er, da det virker som en lidt kreativt omregning, er det en rigtig måde undersøge om grafen har en lodret asymptote i x = -1 ? 

På forhånd tak

En rettelse 

ax² + bx + c opløst i faktorer er a• ( x - x₁ ) • ( x - x₂ ) , og a må jo så være 1

Så udtrykket bliver når jeg indsætter rødderne x = -1 og x = 2 i tælleren og i nævneren x = 1

tælleren     ( x - (-1 )) • ( x - 2)         = ( x + 1 ) • ( x + 2 )

nævneren  ( x  - (-1)) • ( x - ( -1 ))   = ( x + 1 ) • ( x + 1 )

Du har en fortegnsfejl i tælleren

Ja. det er den korrektemetode når du har 0 i både tæller og nævne. Du må også gøre det klart at så er funktionen ikke definere for x = roden; men det betyder ikke noget for grænseovergangen i det værdien ikke spiller nogen rolle

Tak for svaret

I # 8 Peter lind skriver at der er en fortegnsfejl i tælleren det lyder rigtigt, men der er noget med min omforming (metode) der ikke passer:

Der står i bogen:

Der gælder:

Hvis f ( x ) = g ( x ) / h ( x ) er en polynomiumsbrøk, og a er rod i nævneren h ( x ) og ikke i tælleren g ( x ), er linien med ligningen x = a lodret asymptote til grafen for f.

Sætningen følger af, at hvis a er rod i h ( x ) og ikke i g ( x ), vil

               h ( x )  →  h ( a ) = 0 ,    når   x  →  a

mens   

              g ( x )  → g ( a ) ≠ 0 ,      når   x  →  a

Når tælleren går mod et tal, der ikke er 0, og nævneren går imod 0, bliver brøkken et større og større positivt eller negativt tal. Grafen er derfor næsten lodret i nærheden af x = a, og der er så en lodret asymptote.

Jeg mener der er en fortegns fejl i omformning både af  tælleren og nævneren som er markeret med rødt efter det fjerde lighedstegn for der er noget som ikke passer i min omformning af nævneren ( x + 1).

                x²  - x - 2               ( ( x - ( -1 ))  • ( x - 2 )                ( x + 1 ) • ( x - 2 )               x - 2

f ( x ) = ------------------- =  --------------------------------------  = ------------------------------- =  -------------- 

               x² + 2x + 1           ( ( x - ( - 1 ))• (( x - ( -1 ))               ( x + 1 ) • ( x + 1 )             x + 1

                                                     - ( - x + 2 )                          2

                                                   -------------------             1 +  -----

    x - 2            - ( -x + 2 )                      x                                  x 

------------  =  ------------------- =  -----------------------  =   ------------------   = -1    når x → ∞  får jeg  

   x  + 1            - ( x - 1 )                 - ( x + 1 )                           -1

                                                   ---------------------            -1   -------

                                                            x                                    x

I tælleren skal der stå -2 og ikke 2

I nævneren  er x + 1  ≠  - ( x - 1 )

Grafen har et hul ved x  = -1 ,     når x  →  -1 går nævneren imod 0 så der må være en lodret asymptote når

  x   → -1 ,                                  ( men der står ikke noget i facitlisten )

Mit spørgsmål er, hvordan skal man undersøge om grafen for

                x² - x - 2

f ( x ) = ------------------ ,     har en lodret asymptote i x = -1, 

               x² + 2x +1

for der er noget galt med min omformning, er der nogen kan vise hvordan man foretager denne undersøgelse ?

På forhånd tak

Der er nogle fortegnsfejl og et manglende tegn i linjen med rød. Denne linje er komplet overflødig. Resultatet for grænseoverganger x -> ∞ er +1.

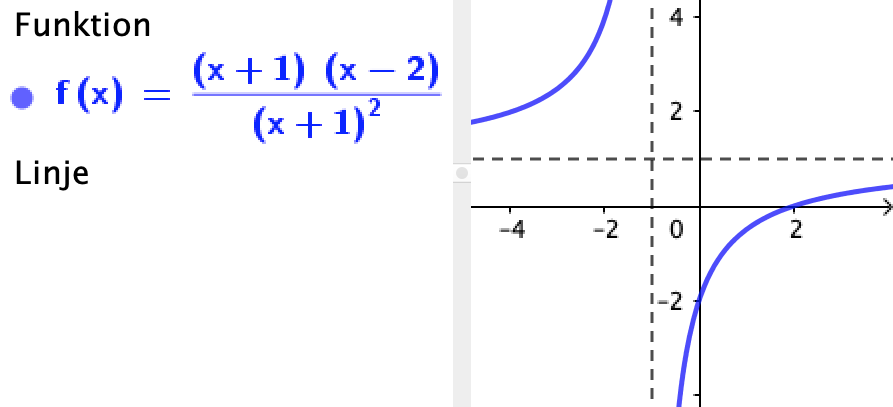
Du skal se på grafen for (x-2)/(x+1) som er i #2. Det er den nemmeste metode. Du kan også prøve at regne på nogle værdier nær ved -1. det kan du gøre meget hurtigt i et regneark.

Tak for svaret

For at undersøge om 

                 x²  - x - 2               ( ( x - ( -1 ))  • ( x - 2 )                ( x + 1 ) • ( x - 2 )               x - 2

f ( x ) = ------------------- =  --------------------------------------  = ------------------------------- =  -------------- 

               x2 + 2x + 1           ( ( x - ( - 1 ))• (( x - ( -1 ))               ( x + 1 ) • ( x + 1 )             x + 1

har lodret i asymptote i x = -1

Funktionen f er ikke defineret i -1, men jeg forsøger lade nogle værdier af x nærme sig  - x fra venstre og højre for at se hvordan funktionsværdierne for funktionen f forløber:

                                                                     Fra venstre                                                 

                   ------------------------------------------------------------------------------------------------------------------ 

                         x                               - 1,1           - 1,01          - 1,001        - 1,0001          - 1,00001               

                    -----------------------------------------------------------------------------------------------------------------

                     tæller:     ( x  - 2 )         - 3,1000     - 3,0100      - 3,001         - 3,00001        - 3,000001  

                     nævner: ( x + 1 )          - 0,1000      -0,0100      - 0,001         - 0,0001          - 0,00001                                                            

                        f ( x )                               31          301              3001             30001             300001       

Tælleren går mod et tal der ikke er 0

Nævneren går imod 0                

Brøken går imod et større positivt tal 

                                                                           Fra højre

                 -------------------------------------------------------------------------------------------------------------------------------

                     x                                   - 0,00009        - 0,00099       - 0,00999     - 0,09999      - 0,99999 

                 ----------------------------------------------------------------------------------------------------------------------------------    

                   tæller:     ( x - 2 )             - 1,9999         - 2,00099         - 2,00999      - 2,09999      - 2,99990 

                  nævner : ( x + 1 )              0,99991         0,999901        0,990010       0,900001     1,000000 • 10^-5

                   f ( x )                              - 2,00027       - 2,00297       - 2,03027       - 2,3332        - 299999 

Tælleren går imod et tal der ikke er 0

Nævneren går imod 1

Brøkken går imod et større negavtiv tal 

Jeg kan se at når x nærmer sig  -1 fra venstre bliver f ( x ) et større og større positivt tal og når x nærmer sig fra højre bliver f ( x ) et større  og større negativt tal:

Fra venstre side                      f ( x )  →  ∞         når     x  →  -1-

Fra højre side                         f ( x )   →  - ∞       når    x  →  -1 + 

Når jeg ser på grafen i svaret # 2 ser det ud til at det passer. 

Det betyder at i nærheden af  x = -1 er grafen næsten lodret også har funktionen f har en lodret asymptote i x = -1

#0. Du har en rationel funktion, dvs. en med et polynomium i tæller og nævner. Du skal fnde evt.  lodrette asymptoter. Gør følgende:

Find rødder i tæller og nævner.

I tilfælde af, at der er rødder i begge polynomier, så skriv tæller og nævner på formen: (x - r₁)·(x - r₂)···, hvor r₁, r₂,...er rødderne i det enkelte polynomium. Reducer herefter brøken. I de led, der står tilbage i nævneren,  erstatter du minus med lighedstegn og får derved de lodrette asymptoter. Dvs. x - r laves om til x = r.

I tilfælde af at der ikke er rødder i nævneren, så er der ingen lodret asymptote. 

Hvis et led på formen (x - r) kan forkortes ud i tæller og nævner, så svsrer det til, at der er et hul på grafen i det punkt.

Tak for svaret