Fysik

Opgave om snorkraft

28. juli 2022 af jonasmåge - Niveau: A-niveau

Hej, er der nogen som kan hjælpe mig igennem disse tre opgaver? Opgaverne er vedhæftet, på forhånd tak :)

Vedhæftet fil: Skærmbillede 2022-07-28 173255.png

Brugbart svar (0)

Svar #1
28. juli 2022 af Eksperimentalfysikeren

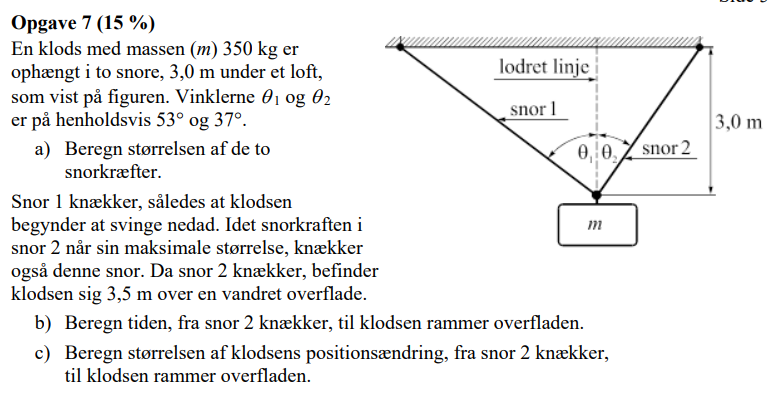
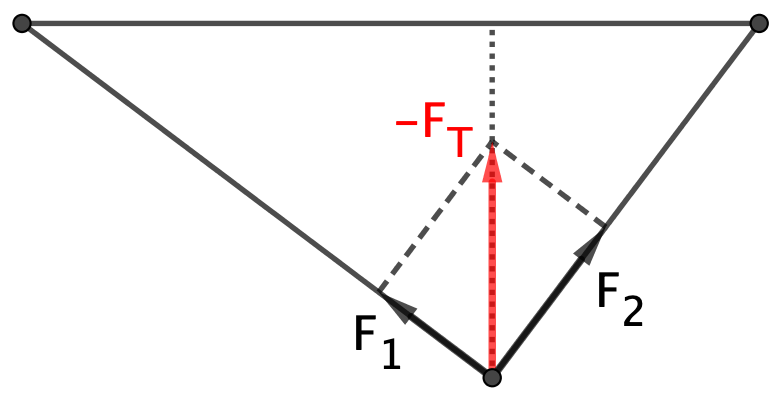
a) De to lodrette komposanter er til sammen lig med tyngdekraften på loddet. De to vandrette komposanter er lige store, men modsatrettede; ellers vil loddet flytte sig.

b) Hvad er du selv kommet frem til her?

c) Afhænger af b)

Brugbart svar (0)

Svar #2
29. juli 2022 af OliverHviid

Eksperimentalfysikeren, det kan godt være at det er mig der forstår opgaven forkert, men ville summen af kræfter i y-retningen (altså de lodrette komposanter) ikke også være 0 idet der ingen bevægelse er?

Brugbart svar (0)

Svar #3
29. juli 2022 af mathon

Brugbart svar (0)

Svar #4
29. juli 2022 af mathon

$\small \begin{array}{lllllll}\textbf{a)}\\&&\theta_1+\theta_2=53\degree+37\degree=90\degree\qquad m\cdot g=(350\;\mathrm{kg})\cdot \left ( 9.82\;\mathrm{\frac{N}{kg}} \right )=3437\;\mathrm{N}\\\\&&F_1=m\cdot g\cdot \frac{\sin(\theta_2)}{\sin(\theta_1+\theta_2)}\qquad F_2=m\cdot g\cdot \frac{\sin(\theta_1)}{\sin(\theta_1+\theta_2)}\\\\&& F_1=\left (3437\;\mathrm{N} \right )\cdot \sin(37\degree)=2068.44\;\mathrm{N}\\\\&& F_2=\left (3437\;\mathrm{N} \right )\cdot \sin(53\degree)=2744.91\;\mathrm{N} \end{array}$

Brugbart svar (0)

Svar #5
29. juli 2022 af Eksperimentalfysikeren

#2 Jo, det er mig, der ikke har udtrykt mig præcist. Vektorsummen af de tre kræfter skal være 0. Derfor skal størrelsen af summen af de to snorekræfter være lig med størrelsen af tyngdekraften.

Brugbart svar (0)

Svar #6
31. juli 2022 af mathon

$\small \begin{array}{lllllll}\textbf{b)}\\& \textup{L\o s}\\&& \frac{1}{2}\cdot g\cdot t^2=3.5\;\mathrm{m} \end{array}$

Brugbart svar (0)

Svar #7
01. august 2022 af mathon

$\small \textbf{c)}$
Snorkraften i snor 2 når sin maksimale størrelse i højre yderpunkt
efter at have tilbagelagt vinklen $\small 2\theta _2$ med radius $\small r=\frac{3\;\mathrm{m}}{\cos(\theta _2)}=\frac{3\;\mathrm{m}}{\cos(37\degree)}$

Klodsens positionsændring:
$\small \begin{array}{ll} p=2\cdot \left ( r\cdot \sin\left ( \theta _2 \right ) \right )=2\cdot \left ( \frac{3\;\mathrm{m}}{\cos(\theta _2)}\cdot \sin\left ( \theta _2 \right ) \right )=6\cdot \tan(\theta_2)\;\mathrm{m}=6\cdot \tan(37\degree)\;\mathrm{m}=4.52\;\mathrm{m} \end{array}$

Brugbart svar (0)

Svar #8
01. august 2022 af Soeffi

#0. Illustration til a)...

Vedhæftet fil:snorkraft.png

Brugbart svar (0)

Svar #9
02. august 2022 af Eksperimentalfysikeren

Snorekraften er størst når snoren er lodret. Her virker hele tyngdekraften i snorens retning og centrifugalkraften er størst.

Her er klodsen kommet længere ned idet snoren er længere end de 3m, klodsen var under "loftet". Snorens længde er r=3m/cos(37º). Det stykke, klodsen er kommet ned er r-3m. Derved har den fået omsat potentiel energi til kinetisk energi, hvoraf man kan finde hastigheden v.

Derefter falder klodsen og størrelsen af positionsændringen skal beregnes. Da der står "størrelsen" regner jeg med, at der menes afstanden mellem det sted, hvor klodsen slipper fri, og det sted, hvor den lander. Højden er opgivet til 3m. Den vandrette afstand fås ved at gange v med den tid, der er fundet i b). Til sidst bruges afstandsformlen.

Bemærk: Jeg er ikke helt sikker på fortolkningen af "størrelsen af klodsens positionsændring" Uanset, hvordan du selv fortolker det (og bruger fortolkningen i løsningen) bør du skrive, hvordan du fortolker det.

Brugbart svar (0)

Svar #10
04. august 2022 af mathon

For at fjerne en evt. og forståelig forvirring i forbindelse med ovenstående,
skal det tilføjes, at jeg tog fejl i angivelse af maksimal snorkraft i en yderstilling.
Den maksimale snorkraft er i ligevægtsstillingen (hvor afstanden til loft er størst), som angivet i #9.

Skriv et svar til: Opgave om snorkraft

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.