Matematik

Projektion af punkt på linje

20. november 2022 af Adl9 - Niveau: A-niveau

Har brug for akuut hjælp, til nedenstående opgave!

Vedhæftet fil: billede_2022-11-20_184544756.png

Brugbart svar (0)

Svar #1
20. november 2022 af peter lind

Brugbart svar (0)

Svar #2
20. november 2022 af peter lind

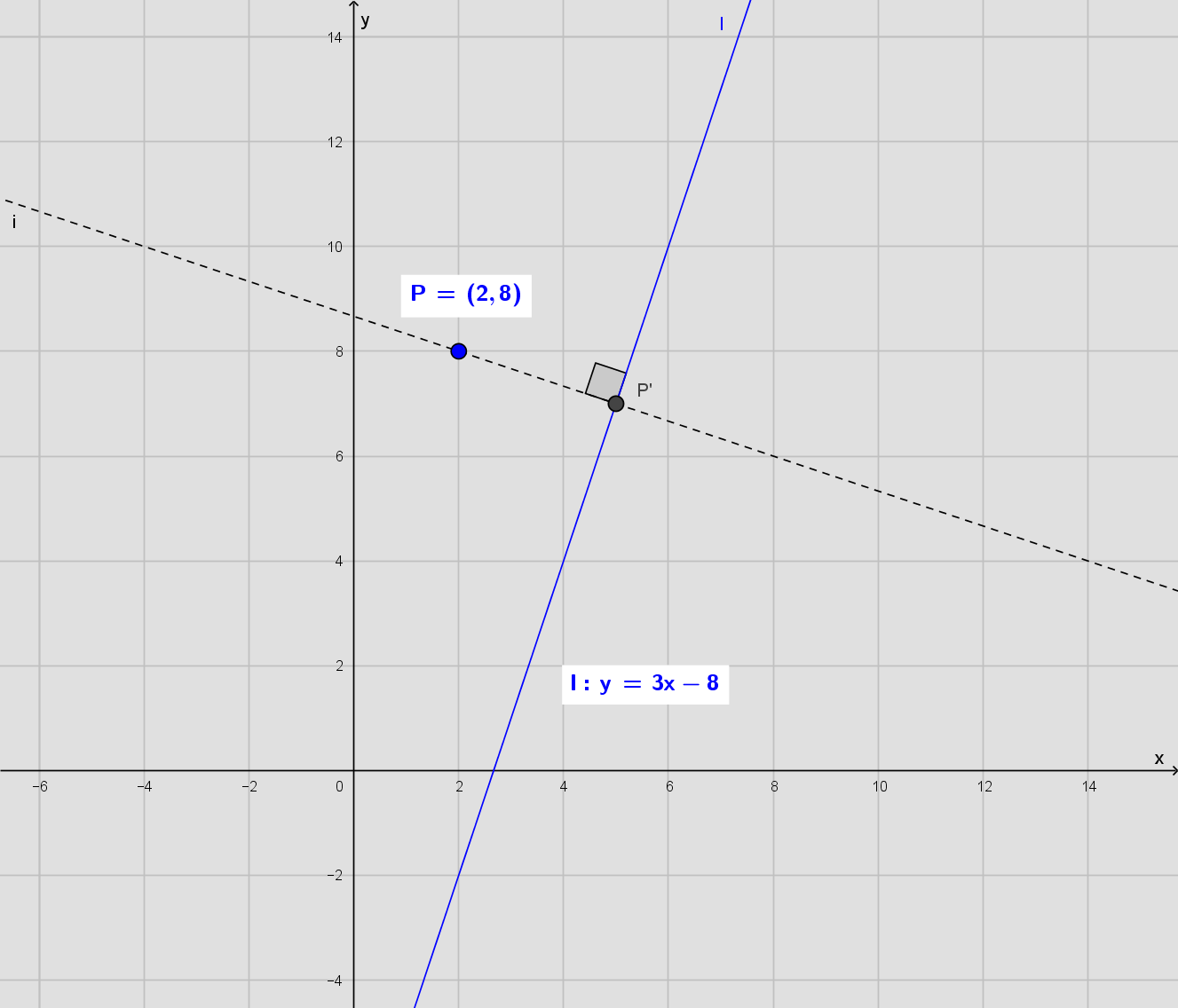
Find ligningen for linjen gennem (2, 8) og står vinkelret på l. Der hvor de to linjer skærer hinanden er det søgte punkt

Brugbart svar (0)

Svar #3
20. november 2022 af Soeffi

#0. Løst i Geogebra.

Vedhæftet fil:linje.png

Brugbart svar (0)

Svar #4
20. november 2022 af ringstedLC

eller:

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #5
20. november 2022 af SuneChr

Kald P's projektion på $l$ for P₀ = (x₀ , 3x₀ - 8)
Retningsvektor r for $l$ er (1 , 3)
Vi har nu til bestemmelse af x₀ :
P₀P • r = 0

Brugbart svar (0)

Svar #6
21. november 2022 af Soeffi

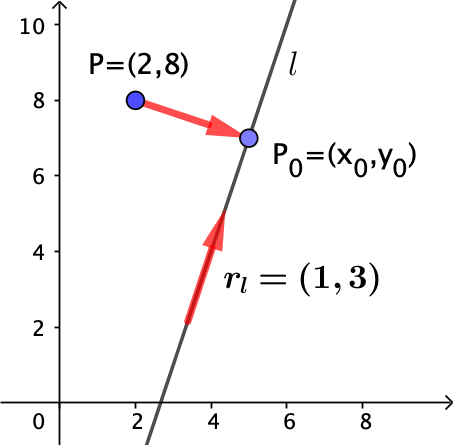
#0. (I forlængelse af #5 og med hjælp fra nedenstående tegning...):

$y=3x-8\Leftrightarrow {\color{Red} -3}x+{\color{Red} 1}y+8=0$

En normalvektor til l ses af de røde tal at være n = (-3,1). En retningsvektor, r_l, til l er dermed minus tværvektoren til n, som giver r_l = (1,3). (Minus tværvektoren vælges fordi, at den er pænere end tværvektoren selv.)

$\overrightarrow{PP_0}\cdot \overrightarrow{r_l}=0 \Rightarrow \begin{pmatrix} x_0-2\\(3x_0-8)-8 \end{pmatrix} \cdot \begin{pmatrix} 1\\3 \end{pmatrix}=0\Leftrightarrow$

$x_0-2+3((3x_0-8)-8)=0\Leftrightarrow 10x_0-50=0\Leftrightarrow x_0=5\Rightarrow y_0=3\cdot 5-8=7.$

Dermed har man at...

$P_0=\begin{pmatrix} 5\\7 \end{pmatrix}$

Vedhæftet fil:linje2.png

Skriv et svar til: Projektion af punkt på linje

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.