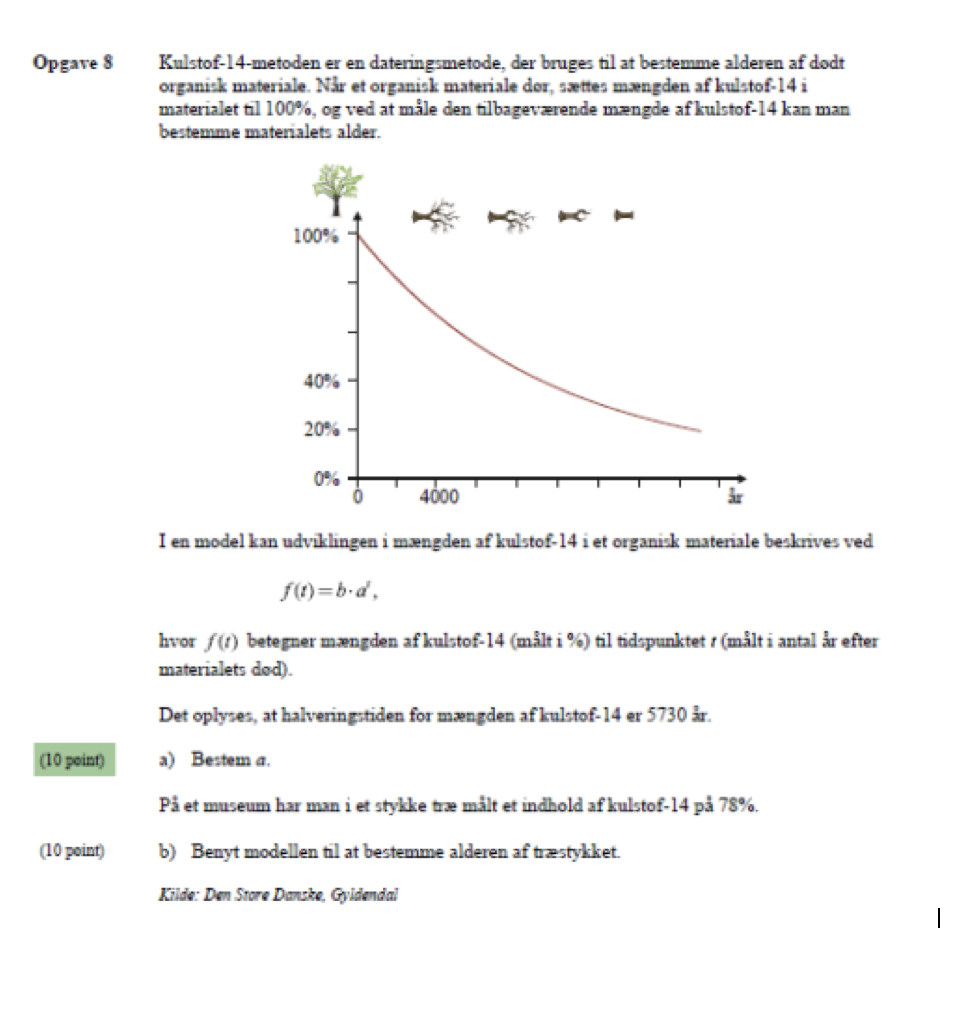
Matematik

bestem a ved hjælp af halveringstiden

30. januar 2023 af emily2020 - Niveau: C-niveau

Hej jeg har fået denne opgave (vedhæftet fil)

Jeg har brug for hjælp til både opgave a og b håber nogen kan hjælpe!

Vedhæftet fil: Skærmbillede 2023-01-30 kl. 16.14.41.png

Brugbart svar (0)

Svar #1
30. januar 2023 af peter lind

Brugbart svar (0)

Svar #2
30. januar 2023 af peter lind

a) se formel 94 side 16 i din formelsamling

b) brug formlen i opgaven

Svar #3
30. januar 2023 af emily2020

Tak for svar, men jeg tror ikke vi har samme formelsamling min formel 94 siger noget om logaritmefunktioner

Brugbart svar (0)

Svar #4
30. januar 2023 af peter lind

logaritmefunktionen er den inverse til eksponentialfunktionen og den formel jeg henviser til bruger den faktisk

Svar #5
30. januar 2023 af emily2020

Forstår stadigvæk ikke helt hvad jeg skal skrive ind så. Altså hvis jeg skulle gøre det ville jeg nok isolere a i halveringsformlen, men det ved jeg heller ikke helt hvordan eller har prøvet hvor jeg fik a til 11460 men er ikke sikker på det rigtigt…

Brugbart svar (0)

Svar #6
30. januar 2023 af peter lind

Du kan se formlen under eksponentiel aftagende funktioner.

Hvis du vil udlede den

½b = b*a^t <=> ½ = at <=> ln(½) = ln(a)*t <=> t = ln(½)/ln(a) <=> ln(a) = ln(½)/t

a bliver negativ når det er en aftagende funktion

Svar #7
30. januar 2023 af emily2020

Er det her så rigtigt

Vedhæftet fil:Skærmbillede 2023-01-30 kl. 19.14.31.png

Brugbart svar (0)

Svar #8
30. januar 2023 af peter lind

Nej. halveringstiden er ln(½)/ln(a)

Svar #9
30. januar 2023 af emily2020

Men jeg ved jo ikke hvad a er?

Brugbart svar (0)

Svar #10
30. januar 2023 af ringstedLC

Nej, men du kender halveringstiden:

$\begin{align*} t=0 &\Rightarrow 100\%\textup{ C-14} \\ f(0) &= 100\%\cdot a^0=100\% &&,\;a^0=1 \\ f\left(T_{1/2}\right)=\tfrac{1}{2}\cdot f(0)=50\% &= 100\%\cdot a^{T_{1/2}} \\ a^{T_{1/2}} &= \tfrac{50\%}{100\%}=\tfrac{1}{2} \\ \log\left ( a^{T_{1/2}} \right ) &= \log\left ( \tfrac{1}{2} \right ) \\ T_{1/2}\cdot \log(a) &= -\log(2) \\ \\T_{1/2} &= \frac{\log\left ( \frac{1}{2} \right )}{\log(a)} &&,\;\textup{formel {\color{Red} (110), STX A}} \\ \log(a) &= \frac{\log\left ( \frac{1}{2} \right )}{T_{1/2}} \\ a &= 10^{\frac{\log\left ( \frac{1}{2} \right )}{T_{1/2}}} &&,\;\textup{formel {\color{Red} (92), STX A}} \end{align*}$

Angiv korrekt niveau så vores henvisninger passer.

Brugbart svar (0)

Svar #11
30. januar 2023 af peter lind

undskyld

se ln(a) = ln(½)/t

Skriv et svar til: bestem a ved hjælp af halveringstiden

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.