Matematik

Lineære differentialligninger af 1. orden

26. marts 2023 af cecilie1606 - Niveau: A-niveau

Hej

Er der nogle som kan hjælpe mig med denne her opgave?

På forhånd tak for hjælpen.

Vedhæftet fil: Opgave 13.png

Brugbart svar (0)

Svar #1
26. marts 2023 af StoreNord

Mon ikke du kan finde typen her: Jeg ville nok prøve nummer 4.

Vedhæftet fil:20230326_193821.jpg

Svar #2
28. marts 2023 af cecilie1606

Undskyld, men jeg har simpelthen brug for at en forklaring på, hvordan man løser opgaverne.

Jeg er ikke helt med

Brugbart svar (0)

Svar #3
28. marts 2023 af StoreNord

Differentialligningen står til venstre i tabellen, og løsningen står til højre.
For at beregne løsningen skal du i opgavens differentialligning identificere, hvad g(x) og h(x) er samt G(x), som er stamfunktionen til g.
Disse ting skal du indsætte i tabeleksempelplets formel for y.
Derefter skal du regne på udtrykket.

Brugbart svar (1)

Svar #4
28. marts 2023 af M2023

#2. Du skal bruge den nederste løsningsformel.

Her er det underforstået at

$A(x)=\int a(x)\;dx$

Spørgsmål 1. Man får

a(x) = x^-1, b(x) = x^-2 og A(x) = ln(|x|) + k = ln(x) + k (idet x > 0).

Dette indsættes i formlen:

$y=e^{-ln(x)-k}\cdot \int x^{-2} \cdot e^{ln(x)+k}\;dx+c\cdot e^{-ln(x)-k}=$

$e^{ln(x^{-1})}\cdot e^{-k}\cdot \int x^{-2} \cdot e^{ln(x)}\cdot e^{k}\;dx+c\cdot e^{ln(x^{-1})}\cdot e^{-k}=$

$x^{-1}\cdot e^{-k}\cdot \int x^{-2} \cdot x\cdot e^{k}\;dx+c\cdot x^{-1}\cdot e^{-k}=$

$x^{-1}\cdot e^{-k}\cdot e^{k}\cdot \int x^{-2} \cdot x\;dx+c\cdot e^{-k}\cdot x^{-1}=$

$x^{-1}\cdot \int x^{-1} \;dx+c\cdot e^{-k}\cdot x^{-1}=$

$x^{-1}\cdot (ln(x)+k')+c\cdot e^{-k} \cdot x^{-1}=$

$x^{-1}\cdot \left (ln(x)+k'+c\cdot e^{-k} \right )=$

$x^{-1}\cdot \left (ln(x)+C \right )$

Svar #5
28. marts 2023 af cecilie1606

#3
Differentialligningen står til venstre i tabellen, og løsningen står til højre.
For at beregne løsningen skal du i opgavens differentialligning identificere, hvad g(x) og h(x) er samt G(x), som er stamfunktionen til g.
Disse ting skal du indsætte i tabeleksempelplets formel for y.
Derefter skal du regne på udtrykket.

Okay super! Mange tak for svar :)

Jeg har 2 spørgsmål:

1. Hvorhenne er det man kan "se" i udregningen, at løsningen til differentialligningen, har en graf, som går gennem punktet (1,2)?

2. Ved opgave 2, vender man så fortegnene nu hvor formlen er y' - a(x)*y=b(x) ?

Brugbart svar (0)

Svar #6
28. marts 2023 af StoreNord

1) Du har fundet en generel løsning. Den skulle gerne indeholde et ekstra led, som er +c.
For at finde netop den søgte løsning, skal du for en bestem x-værdi beregne c, hvor
"Generel løsning"(1) + c = 2; altså:

$\frac{1}{x}\cdot C = 2$ hvor x=1

2) Her skal du bare lave en ny beregning.

Brugbart svar (0)

Svar #7
28. marts 2023 af StoreNord

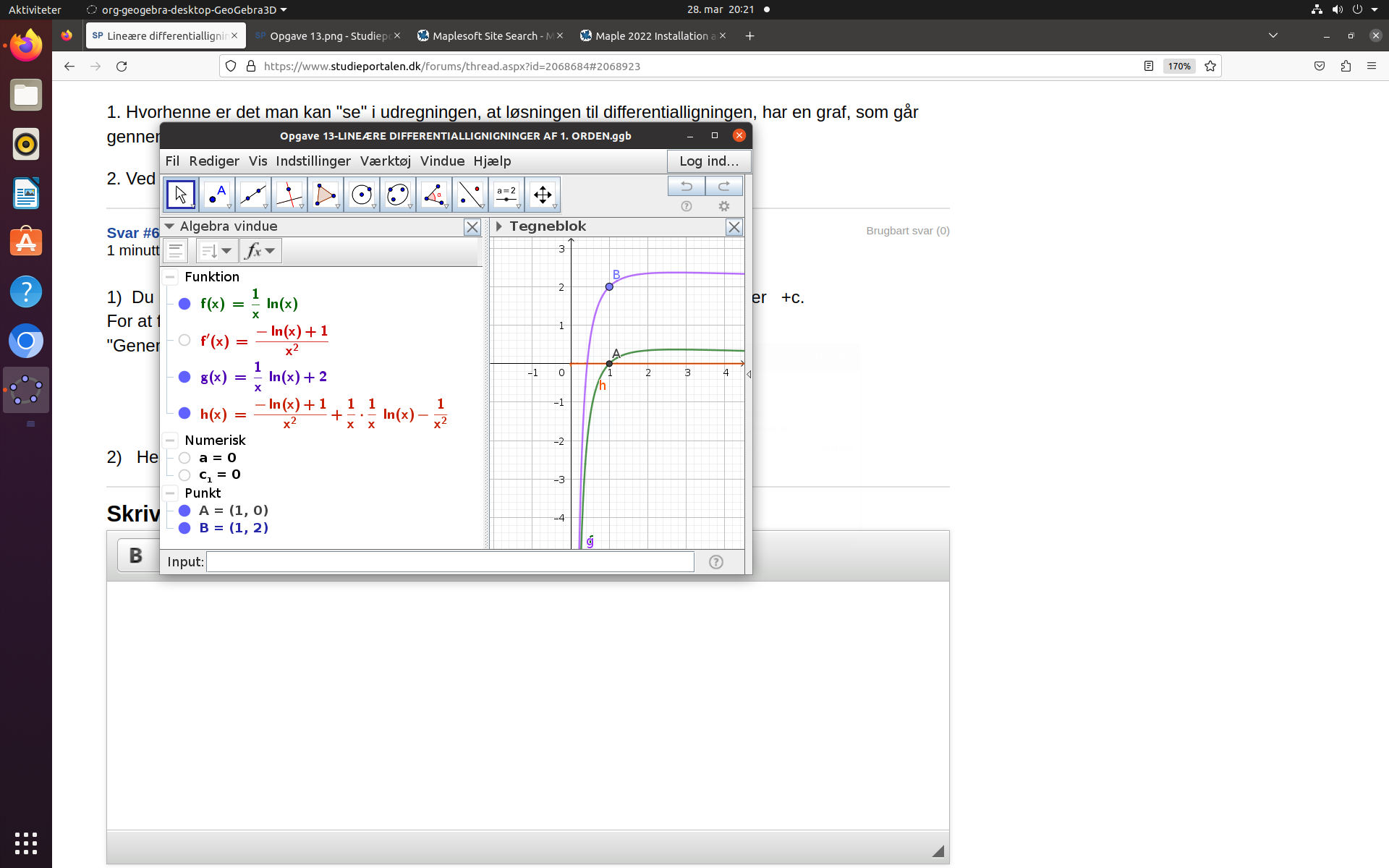
Jeg har kun beregnet a). h(x) er en kontrol.beregning af differentialligningen.
f(x) er den generelle løsning, og g(x) er den specifikke.

Vedhæftet fil:Skærmbillede fra 2023-03-28 20-21-58.png

Svar #8
28. marts 2023 af cecilie1606

#6 Men vil det sige, at hvis jeg tager udgangspunkt i #4 udregningen. Så skal jeg på den nederste linje indsætte 1 ind på x's plads og sætte = 2, eller er det helt forkert forstået?
Eller har denne udregning slet ikke noget at gøre med den generelle løsning?

Undskyld, men jeg er stadig lidt usikker på opgaven...

Brugbart svar (0)

Svar #9
28. marts 2023 af StoreNord

For at finde den generelle løsning skal du ikke tænke på punktet (1,2), men blot skrive +C.
Men du bliver her spurgt om den specifikke løsning, som går gennem (1,2). Så skal du beregne C,

for at få grafen "på plads".

Brugbart svar (0)

Svar #10
28. marts 2023 af StoreNord

I #6 skulle der have stået:
$\frac{1}{x}\cdot ln(x) + C = 2$
eller som #4 skrev:
$x^{-1}\cdot \left (ln(x)+C \right )$
men så er det ikke den samme C.

Brugbart svar (0)

Svar #11
28. marts 2023 af ringstedLC

#8 #6 Men vil det sige, at hvis jeg tager udgangspunkt i #4 udregningen. Så skal jeg på den nederste linje indsætte 1 ind på x's plads og sætte = 2, eller er det helt forkert forstået?

Korrekt, og så løser du den ligning.

Brugbart svar (0)

Svar #12
28. marts 2023 af ringstedLC

#8

Undskyld, men jeg er stadig lidt usikker på opgaven...

Du behøver ikke at undskylde noget, emnet diff.-ligninger kan virke noget mærkeligt til en begyndelse. Årsagen til de to typer løsninger, generel og specifik, skyldes at der integreres på begge af lighedstegnet for at løse ligningen. Det afstedkommer en integrationskonstant c. Et simpelt eksempel:

$\begin{align*} \textup{Diff.-lign.}:y' &= 2x \\ \int \!y'\,\mathrm{d}y &= \int \!2x\,\mathrm{d}x \\ y &= x^2+c &&\textup{Generel\,l\o sn.} \\ \textbf{L\o sningen\,er\,en\,parabel}\\\textbf{beligg.\,sym.\,om\,\textit{y}-aksen.} \\\textup{Pr\o ve}:\\ y'=\bigl(x^2+c\bigr)' &= \bigl(x^2\bigr)' \\&=2x^{2\,-\,1} \\y' &= 2x \\\\ y\;\textup{gennem fx }(1,2):2 &= 1^2+c &&\Rightarrow c=1 \\&&&\Rightarrow y=x^2+1 &&\textup{Specifik\,l\o sn.}\\ y\;\textup{gennem fx }(3,5):5 &= 3^2+c &&\Rightarrow c=-4 \\&&&\Rightarrow y=x^2-4 &&\textup{Specifik\,l\o sn.} \end{align*}$

Formelsamlingen giver derfor (nogle) kun generelle løsninger. En opgave har måske en betingelse for den generelle løsning som så giver en specifik løsning.

Svar #13
29. marts 2023 af cecilie1606

Vil det sige, at dette er rigtigt forstået ift. opgave 1?

Vedhæftet fil:Opgave 1.png

Brugbart svar (1)

Svar #14
29. marts 2023 af StoreNord

Ja, det er rigtigt forstået.
Næstsidste linje kunne være :
"Dvs, dén specifikke løsning, der går gennem punktet (1,2) er:"

Svar #15
29. marts 2023 af cecilie1606

Okay super!
Mem skal lige høre ved opgave 2, er det så den sammen fuldstændige løsning jeg skal bruge, eller hvor finder jeg den henne, for den står ikke i formelsamlingen, når der nu står et minus i stedet for et plus?
Altså den hedder vel:
y'-a(x)×y=b(x)
Men så ændre den fuldstændige løsning sig vel også, eller hvordan skal det forstås?

Svar #16
29. marts 2023 af cecilie1606

Jeg fik det til :)

Mange tak for hjælpen til jer alle!

Brugbart svar (0)

Svar #17
30. marts 2023 af StoreNord

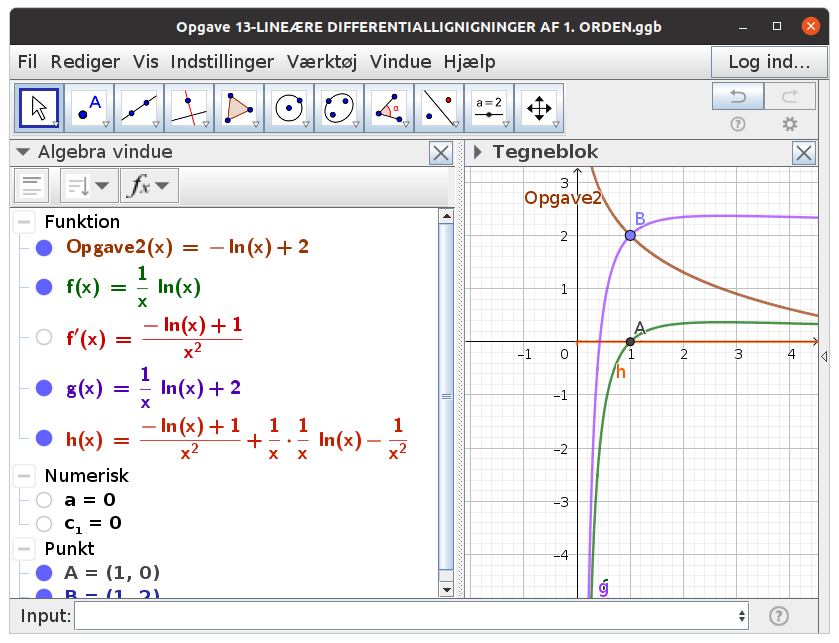
Den brune her?

Vedhæftet fil:Skærmbillede fra 2023-03-30 01-23-22.png

Skriv et svar til: Lineære differentialligninger af 1. orden

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.