Matematik

Kvadratisk programmering

26. november 2023 af coronanana - Niveau: A-niveau

Har akut brug for hjælp. Nogen der kan forklare dette?

Vedhæftet fil: Billede111.png

Brugbart svar (0)

Svar #1
27. november 2023 af mathon

Brugbart svar (0)

Svar #2
27. november 2023 af mathon

$\begin{array}{llllll} \textbf{a)}\\&\textup{Det samlede}\\& \textup{d\ae kningsbidrag:}\\&& p_1\cdot x-10\cdot x+p_2\cdot y-10\cdot y\\\\&& \left (-0.50x+60 \right )\cdot x-10x+\left (-0.10y+40 \right )\cdot y-10y\qquad 0< x+y\leq 140\\\\&& -0.50x^2+50x -0.10y^2+30y=\\\\&& -0.50\left ( x^2-100x \right )-0.10\left ( y^2-300y \right )=\\\\&& -0.50\left ( x-50 \right )^2+2500-0.10\left ( y-150\right)^2+22500=\\\\&& -0.50\left ( x-50 \right )^2-0.10\left ( y-150\right)^2+25000\\\\&\textup{hvoraf}\\&& N(0)=-0.50\left ( x-50 \right )^2-0.10\left ( y-150\right)^2+25000=0\\\\&& \frac{\left ( x-50 \right )^2}{2}+\frac{\left (y-150 \right )^2}{10}=25000\\\\\\&& \frac{(x-50)^2}{(100\sqrt{5})^2}+\frac{(y-150)^2}{500^2}=1 \end{}$

Svar #3
27. november 2023 af coronanana

Er det samlede dækningsbidrag 25000?

Hvad står 1 for?

Svar #4
27. november 2023 af coronanana

Er det samlede dækningsbidrag 25000?

Hvad står 1 for?

Brugbart svar (0)

Svar #5
27. november 2023 af M2023

#0. Du skal bruge Hallings formler:

Du har, at DB(x,y) = p₁·x - 10·x + p₂·y - 10·y = t ⇒ DB(x,y) = -0,5·x² + 50·x - 0,1·y² + 30·y = t

Brugbart svar (0)

Svar #6
27. november 2023 af M2023

#5 er angående a) og b). Angående c): Dette er en løsning i Geogebra:

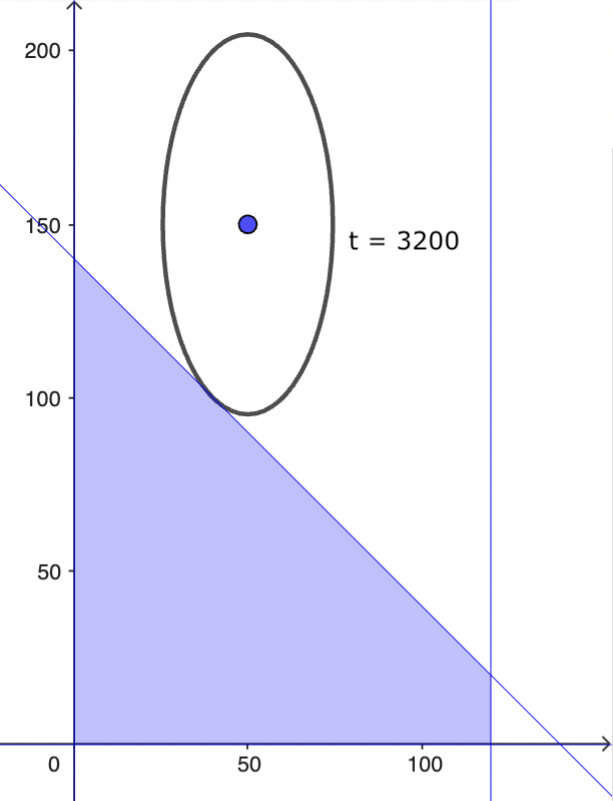
Løsningen er det punkt, hvor niveaukurven rører ved polygonområdet. Bemærk: Jo større dækningsbidrag, jo mere samler ellipsen sig om (x,y) = (50,150).

Vedhæftet fil:ellipse.png

Brugbart svar (0)

Svar #7
27. november 2023 af M2023

#6. Jeg kan lige nævne, at optimumspunktet er (x,y) = (40,100).

Brugbart svar (0)

Svar #8
27. november 2023 af M2023

#0. Bemærk venligst:

DB(x₀,y₀) er dækningsbidraget i punktet (x₀,y₀). Dette er et tal, som for nemheds skyld kaldes t.

N(t) er en punktmængde, nemlig mængden af punkter (x,y) for hvilke DB(x,y) = t.

Skriv et svar til: Kvadratisk programmering

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.