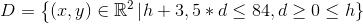Matematik
Optimeringsopgave ved hjælp af lagranges metode og eliminering.
Hej Studieportalen,
Så sidder jeg igen her en sen nattetime og kan ikke forstå hvad det er jeg skal foretage mig her, opgaven er som følger:
Postvæsnet i langbortistan ekspedere kun såkaldte ruller - altså pakker i cylinderform - Hvis summen af længden l og tre en halv gange diameteren er højest 84 cm. Hvad er den maksimale volumen af sådan en rulle?
Redegør for at opgaven kan løses ved at bestemme maksimum for en funktion V(l,d) defineret på en lukket og begrænset delmængde af R^2 (optimering under bibetingelse). Løs dette problem med begge metoder, altså dels ved elimination af en af de variable og dels med Lagranges metode.
Jeg vil meget gerne guides igennem hvordan dette skal redegøres for. Jeg forstår det simpelthen ikke. Det er måske søvn der tynger mig.
Svar #1
06. november 2012 af Andersen11 (Slettet)
Cylinderen er givet ved sin længde h og diameter d. Rumfanget af en sådan cylinder er
V = π·(d/2)2·h
Postvæsenet har sat en betingelse for at forsende sådan en cylinfer, nemlig at
h + (7/2)·d ≤ 84 .
Da der skal være tale om en fysisk realiserbar cylinder, skal der også gælde
h ≥ 0 og d ≥ 0
I (d,h)-planen skal vi altså finde maksimum for V p polygonområdet begrænset af linierne med ligningerne
h = 0, d = 0, og h = -(7/2)·d + 84 .
Funktionen V(d,h) = π·(d/2)2·h har ingen stationære punkter i det indre af polygonområdet, så det er klart, at dens maksimum må antages på linien
h = -(7/2)·d + 84 , 0 ≤ d ≤ 2·84/7 = 24 .
På denne linie har vi
V(d,h) = π·(d/2)2·h = π·(d/2)2·(84 - (7/2)d) = 21πd2 - (7π/8)d3 ,
der klart ses at have maksimum for d = 16 , med tilhørende h = 28 .
Svar #3
15. januar 2015 af jan12344 (Slettet)
Hvordan ville du løse denne opgave vha. Lagranges metode.
Svar #6
19. januar 2015 af kjsahdsh (Slettet)
Ok jeg forstår Det skal være d ≥0, h ≥0. Men må de egentlig gerne være 0? Skal det ikke hellere være d>0 og h>0?
Svar #7
19. januar 2015 af Andersen11 (Slettet)
#6
Det er nok klart, at d = 0 eller h = 0 fører til en løsning med volumen V = 0 , der ikke er særligt anvendeligt i praksis. Men ved at medtage d = 0 eller h = 0 får vi, at V(d,h) er defineret på en begrænset og afsluttet delmængde af R2 , så det vides, at der findes et globalt maksimum.
Svar #8
31. oktober 2020 af naturVstudent
#1Cylinderen er givet ved sin længde h og diameter d. Rumfanget af en sådan cylinder er
V = π·(d/2)2·h
Postvæsenet har sat en betingelse for at forsende sådan en cylinfer, nemlig at
h + (7/2)·d ≤ 84 .
Da der skal være tale om en fysisk realiserbar cylinder, skal der også gælde
h ≥ 0 og d ≥ 0
I (d,h)-planen skal vi altså finde maksimum for V p polygonområdet begrænset af linierne med ligningerne
h = 0, d = 0, og h = -(7/2)·d + 84 .
Funktionen V(d,h) = π·(d/2)2·h har ingen stationære punkter i det indre af polygonområdet, så det er klart, at dens maksimum må antages på linien
h = -(7/2)·d + 84 , 0 ≤ d ≤ 2·84/7 = 24 .
På denne linie har vi
V(d,h) = π·(d/2)2·h = π·(d/2)2·(84 - (7/2)d) = 21πd2 - (7π/8)d3 ,
der klart ses at have maksimum for d = 16 , med tilhørende h = 28 .
Hvorfor er det klart at d = 16 og h = 28?
Skriv et svar til: Optimeringsopgave ved hjælp af lagranges metode og eliminering.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.