Matematik
Chi i anden
HEJ jeg har en opgave jeg er lidt i tvivl om hvordan jeg skal løse, håber der er nogen der kan hjælpe! - den er vedhæftet ;)
Svar #1
14. maj 2014 af Amril (Slettet)
Hvis du antager, at vælgeradfærden er uændret siden valget, da må du forvente, at en ny meningsmåling vil stemme overens med den samme fordeling af stemmer som ved valget.
Opstil da en tabel med de forventede værdier, og beregn teststørrelsen, den relative kvadratiske afvigelse. Sammenlign med signifikansniveau (find den kritiske værdi ud fra antallet af frihedsgrader og signifikansniveauet).
Svar #2
14. maj 2014 af Manu0407 (Slettet)
Er dette rigtigt?
Svar #5
14. maj 2014 af Amril (Slettet)
Du skal bestemme den kritiske værdi hvis signifikanssandsynlighed er 5 %. Anvend en tabel, som kan findes online. Du får brug for antallet af frihedsgrader.
Er den fundne afvigelse mindre end denne? Hvis ja, befinder vi os i vores acceptområde, og må derfor acceptere nulhypotesen.
Svar #7
14. maj 2014 af SuneChr
Jeg forstår ikke rigtig din summation i # 2. Der har du vedhæftet nogle andre tal i tabellen end i # 0.
I forhold til # 0 :
Parti A 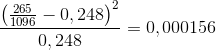
Svar #8
14. maj 2014 af Manu0407 (Slettet)
Det er denne tabel ikke?
Svar #9
14. maj 2014 af Manu0407 (Slettet)
Hvad mener du? Du starter jo med at sige i f.eks. parti A: 0.248*1096=271.808
Så minuser du antallet med det forventede antal og dividere det med det forventede antal altså: (264-271.808)^2/271.808
Det et da sådan man gør??
Skriv et svar til: Chi i anden
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






