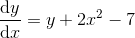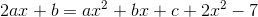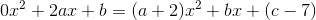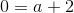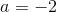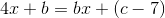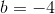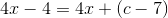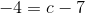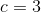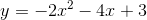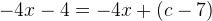Matematik
Bestem andengradspolynomium der er løsning til differentialligningen
28. oktober 2015 af
amalieejlertsen (Slettet)
-
Niveau: A-niveau
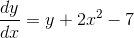
Jeg er med på, at jeg skal indsætte 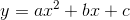 og bestemme koefficienterne i polynomiet, men er der en som kan hjælpe mig påvej step for step? :)
og bestemme koefficienterne i polynomiet, men er der en som kan hjælpe mig påvej step for step? :)
Skriv et svar til: Bestem andengradspolynomium der er løsning til differentialligningen
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







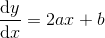 som indsat i differentialligningen
som indsat i differentialligningen