Matematik
Hjælp til grænsen af funktionerne
Jeg skal undersøge funktionerne
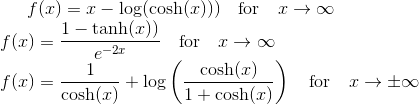
Jeg har prøvet at skrive de forskellige led ud, men jeg ved ikke hvad jeg skal gøre med 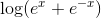 . Kan nogen hjælpe mig?
. Kan nogen hjælpe mig?
Svar #1
16. februar 2016 af Jegharbrugforhjælpp
Og vi må ikke bruge differentiering, da vi ikke er nået dertil endnu. Vi må kun anvende grænseovergange, kontinuitet samt diverse uligheder man kender.
Svar #2
16. februar 2016 af peter lind
log(ex+e-x) = log(ex(1+e-2x) = log(ex)+log(1+e-2x) = x+log(1+e-2x)
Det lyder mærkeligt at du i 3. g endnu ikke har lært om differentiering
Svar #3
16. februar 2016 af Jegharbrugforhjælpp
Jeg har lært at differentiere. Det er et fag på universitetet, hvor vi ikke må differentiere, da vi ikke har vist det endnu.
Kan heller finde frem til grænsen af funktion 3. Jeg har lavet følgende:
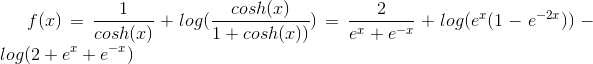
Har sprunget nogle steps over her i denne udregning. Kan ikke rigtig sige noget om grænsen for denne.
Svar #4
16. februar 2016 af peter lind
I dit mellemste led gør som i mit svar i #2 log(ex(1+e-2x) = log(ex)+log(1+e-2x) NB du har vist en fortegnsfejl der.
I det sidste led kan du på samem måde sætte ex ud foran en parentes.
For x -> -∞ dur metoden ikke. Der skal du i stedet sætte e-2x ud foran det hele
Svar #5
16. februar 2016 af peter lind
Du kan slippe nemmere fra tilfældet med x -> -∞ ved at konstatere at f(x) = f(-x)
Svar #6
16. februar 2016 af Soeffi
#0
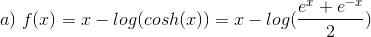
For x → ∞ vil leddet ex dominere og man får :
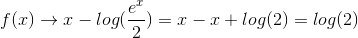
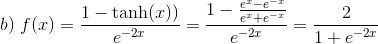
For x → ∞ vil leddet 1 dominere i nævneren og man får :
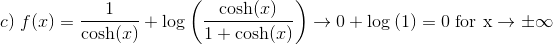
Dette skyldes at nævneren går mod uendelig i første led og at cosh(x) dominerer over 1 i nævneren i det andet.
Svar #9
16. februar 2019 af Herstall
hvordan ville i regne følgende ud:
er lidt usikker på hvordan jeg skal omskrive sinhx da den ikke står direkte som sinhx men sådan lidt mærkeligt som sinh(x^2)-x^2
Svar #10
16. februar 2019 af peter lind
sinh(u) ≈ ½eu for stor og eu -u ≈ eu for u stor så ln(sinh(x2)-x2) = ln(sinh(u) -u)≈ ½u så f(x)-> ∞ for x-> ∞
Svar #11
17. februar 2019 af peter lind
Undskyld der er en fejl i det sidsteDet skal være ln(sinh(u) -u)≈ u +ln(½) så f(x)-> ∞ for x-> ∞
Skriv et svar til: Hjælp til grænsen af funktionerne
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.









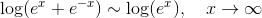
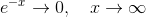
 " menes "er asymptotisk lig med".
" menes "er asymptotisk lig med".