Matematik

Eksponentielle funktioner

28. marts 2017 af PrettyRose (Slettet) - Niveau: A-niveau

Hej, nu sidder jeg med en opgave, som skal laves via screencast i matematik A. Har dog brug for lidt hjælp, der jeg føler mig lost, hvad angår at løse denne opgave. Opgaven lyser således:

Belys begreberne nulpunkter, monotoniintervaller og ekstrema ved hjælp af en analyse af funktion:

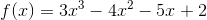f (x) = 3x^3-4x^2-5x+2 og hvor

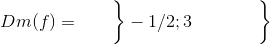
$Dm(f)=\left.\begin{matrix} & & \\ & & \end{matrix}\right\}-1/2;3\left.\begin{matrix} & & & & \\ & & & & \end{matrix}\right\}$

Rigtig mange tak for hjælpen på forhånd :)

Brugbart svar (0)

Svar #1
28. marts 2017 af mathon

      Nulpunkter
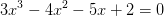
                                 3x^3-4x^2-5x+2=0
det ses, at -1
er en rod
hvoraf:
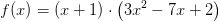
                                 $f(x)=(x+1)\cdot \left ( 3x^2-7x+2 \right )$

monotoniintervalgrænser
bestemmes bl.a. af
$f{\, }'(x)=0$

Svar #2
28. marts 2017 af PrettyRose (Slettet)

Men hvad er ekstrema?

Forstår det ikke rigtigt :/

Brugbart svar (0)

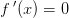
Svar #3
28. marts 2017 af Eksperimentalfysikeren

Ekstrema er fællesbetegnelse for maksima og minima.

Der er to hovedmuligheder for et ekstremum. Det kan være et sted, hvor kurven har vandret tangent, f ' (x) = 0, eller ved endepunktet af et lukket interval. Du skal altså differentiere funktionen og finde nulpunkter af den afledede. Derefter skal du finde fuktionsværdierne for disse x-værdier og for endepunkterne. Hvis intervallet er åbent i den ene ende, er der ikke noget ekstremum i dette punkt, men du kan bruge værdien til at se, om et af de andre er et minimum eller et maksimum.

Brugbart svar (0)

Svar #4
28. marts 2017 af mathon

lokalt max kræver for $f{\, }'(x)$ fortegnsvariationen
$+\; \; 0\; \; -$ i en lille omegn om intetvalgrænseværdien

lokalt min kræver for $f{\, }'(x)$ fortegnsvariationen
$-\; \; 0\; \; +$ i en lille omegn om intetvalgrænseværdien

Skriv et svar til: Eksponentielle funktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.