Matematik

Vektorer 3D

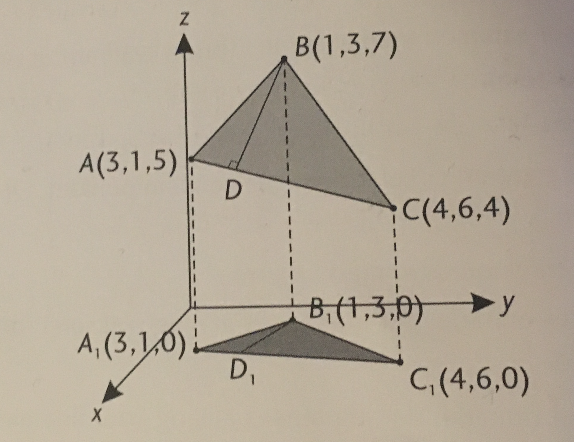
13. januar 2018 af Mikkeldkdk - Niveau: A-niveau

På figuren nedenfor ses en trekant ABC samt projektionen A1B1C1 af trekanten på xy-planen. Endvidere ses fodpunktet D for hjden fra B i trekant ABC samt projektionen D1 af D på xy-planen

b) Bestem koordinatsættet til D

c) Undersg, om B1D1 er højde i trekant A1B1C1

Hvordan laver jeg de to her?

Brugbart svar (0)

Svar #1
13. januar 2018 af StoreNord

Du glemte figuren.

Svar #2
13. januar 2018 af Mikkeldkdk

Ja det gjorde jeg vidst. Den er her

Vedhæftet fil:Skærmbillede 2018-01-13 kl. 20.23.07.png

Brugbart svar (0)

Svar #3
13. januar 2018 af mathon

Brugbart svar (0)

Svar #4
13. januar 2018 af mathon

$\small \overrightarrow{AD} \textup{ er } \overrightarrow{AB}'s \text{ projektion p\aa }\; \overrightarrow{AC}.$

Brugbart svar (0)

Svar #5
13. januar 2018 af ringstedLC

Lav en tegning som i vedhæftede.

Vedhæftet fil:A_M_001 - Vektorer 3D_Mikkeldkdk.png

Svar #6
13. januar 2018 af Mikkeldkdk

Forstår bare ikke hvordan jeg finder D's kordinat

Brugbart svar (0)

Svar #7
13. januar 2018 af StoreNord

Se #4

Svar #8
13. januar 2018 af Mikkeldkdk

Ja forstår godt lidt meningen men ikke helt. Har udregnet AB's projektion på AC. Hvad skal jeg gøre herfra?

Brugbart svar (0)

Svar #9
13. januar 2018 af StoreNord

Denne vektor skulle vise vej fra A til D.

Svar #10
13. januar 2018 af Mikkeldkdk

Skal jeg trække mit oprindelige A fra denne projektion AB på AC?

Brugbart svar (1)

Svar #11
13. januar 2018 af StoreNord

Nej. For at finde Ds position skal du laegge den fundne projektion til punktet A

Svar #12
13. januar 2018 af Mikkeldkdk

Okay tak. Hvordan ved jeg om B1 og D1 er højde i trekant A1B1C1?

Brugbart svar (0)

Svar #13
13. januar 2018 af StoreNord

Check om vinklen er 90 grader.

Som du nok kan se, projiceres punkter direkte ned ved at x-komposanten nulstilles.

Svar #14
13. januar 2018 af Mikkeldkdk

Hvordan tjekker jeg om vinklen er 90 grader midt inde i en trekant?

Brugbart svar (0)

Svar #15
13. januar 2018 af StoreNord

Hvis Ds projektion ikke ligger paa en side af en trekant, er det ihvertfald ikke fodpunkt for en hojde!

Hvad fik du AB projektionen til?

Brugbart svar (0)

Svar #16
14. januar 2018 af mathon

$\overrightarrow{AD}=\left (\frac{\overrightarrow{AB}\cdot \overrightarrow{AC}}{\overrightarrow{AC}^2} \right )\cdot \overrightarrow{AC}=\begin{pmatrix} \frac{2}{9}\\ \frac{10}{9} \\ -\frac{2}{9} \end{pmatrix}$

$\small \overrightarrow{OD}-\overrightarrow{OA}=\begin{pmatrix} \frac{2}{9}\\ \frac{10}{9} \\ -\frac{2}{9} \end{pmatrix}$

$\small \overrightarrow{OD}=\begin{pmatrix} \frac{2}{9}\\ \frac{10}{9} \\ -\frac{2}{9} \end{pmatrix}+\overrightarrow{OA}=\begin{pmatrix} \frac{2}{9}\\ \frac{10}{9} \\ -\frac{2}{9} \end{pmatrix}+\begin{pmatrix} 3\\1 \\ 5 \end{pmatrix}=\begin{pmatrix} \frac{29}{9}\\\frac{19}{ 9} \\ \frac{43}{9} \end{pmatrix}$

$\small D=\left ( \tfrac{29}{9},\tfrac{19}{9},\tfrac{43}{9} \right )\; \; \; \; \; \textup{da et punkt har samme koordinater som sin stedvektor.}$

$\small D_1=\left ( \tfrac{29}{9},\tfrac{19}{9},0 \right )$

$\small \textup{Det unders\o ges, \textbf{}{\color{Red} om} }\overrightarrow{B_1D_1}\textup{ er ortogonal p\aa \ }\overrightarrow{A_1C_1}$
$\small \textup{hvilket kr\ae ver:}$

$\small \overrightarrow{B_1D_1}\cdot \overrightarrow{A_1C_1}=0$

Svar #17
14. januar 2018 af Mikkeldkdk

#16 forstår ikke hvad du mener?

Svar #18
14. januar 2018 af Mikkeldkdk

#15

Jeg fik projektionen af AB på AC =[2/9][10/9][−2/9]

Brugbart svar (0)

Svar #19
14. januar 2018 af StoreNord

Det kan jeg ikke lige tolke, jeg har fået projektionen til:
$\begin{pmatrix} 3\\ 1\\ 5 \end{pmatrix}+\frac{2}{9}\begin{pmatrix} 1\\ 5\\ -1 \end{pmatrix}=\frac{1}{9}\begin{pmatrix} 29\\ {\color{Magenta} 19}\\ 43 \end{pmatrix}$

#16 har fået næsten det samme. Og du har fået det samme som Mathon. To mod een.
Okay I får ret jeg havde læst mit eget 19 som 11. :)

Svar #20
14. januar 2018 af Mikkeldkdk

[[((29)/(9))][((19)/(9))][((43)/(9))]]

Det er den rigtige, skrev vidst forkert

Skriv et svar til: Vektorer 3D

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.