Matematik

Statistik og funktioner

18. juli 2018 af Slashdash - Niveau: Universitet/Videregående

Hej SP. Jeg er i gang med at løse nogle opgaver fra nettet her i sommerferien, og er gået i stå. Jeg har fået givet en funktion:

$N(t)=\frac{M}{(D+C-t)}-\frac{M}{D+C}$

hvor C er givet ved: $C=\frac {\sqrt{D(D+4)}-D}{2}$ .

Denne funktion N beskriver mængden af arbejde man har lagt i en opgave/lektie efter t dage. M er den totale mængde arbejde, der kræves for at udføre opgaven/lektien og D er det totale antal dage man har til at fuldføre opgaven/lektien.

Jeg har tre opgaver, som jeg gerne vil have hjælp til. Jeg har dog specielt svær ved de sidste to opgaver.

1) For store værdier af D find C

Denne opgave er jeg lidt i tvivl om. Jeg ved, at der er tale om en hyperbolsk funktion, og mit bedste bud er at undersøge grænseværdien, når D går mod uendelig. Vil dette give det rigtige resultat, eller skal jeg lave noget algebraisk manipulering?

I de næste to opgaver er jeg helt fortabt, og jeg ville værdsætte enhver form for hjælp.

2) Definer $f(t)=\frac {N(t)}{M}$ som den procentvise færdiggørelse af en opgave efter $t$ antal dage. Udtryk $f(t)$ vha. parametrene p og u under følgende transformationer: $\left\{\begin{matrix} p= \frac{D+C}{D}\\u=\frac{t-a}{b-a} \end{matrix}\right.$

Værdierne af $a$ og $b$ kan findes ved at undersøge randbetingelserne ved $t=0$ og $t=D$ . Udtrykket for $f(t)$ du fandt kan anses som at være fordelingsfunktionen der beskriver andelen af udført arbejde af en opgave mellem $t=a$ og $t=b$

3) Under anvendelsen af resultatet i opg. 2) skal den forventet værdi af tiden $t$ findes i intervallet $a\leq t\leq b$ mht. $p$ og $D$ . Udtryk den forventede værdi mht. D når D er stor.

Brugbart svar (0)

Svar #1
19. juli 2018 af StoreNord

Lad os se på C² i stedet for C:

$\\C=\frac{\sqrt{D(D+4})-D}{2}\Leftrightarrow \\2C+D=\sqrt{D(D+4)}\Leftrightarrow \\4C^{2}+D^{2}+4CD=D^{2}+4D\Leftrightarrow \\C^{2}=D-CD$

Af grafen for C kan man se, at grænseværdien er C=1.

Da C for D>0 altid er mindre end 1, vil andet led altid være mindre end første led.
C² kan altså aldrig blive 1 eller mere.
Det samme må gælde for C.

Da C aldrig blir

Brugbart svar (0)

Svar #2
19. juli 2018 af StoreNord

Ignorèr den sidste linje.

Svar #3
19. juli 2018 af Slashdash

#1
Lad os se på C² i stedet for C:

$\\C=\frac{\sqrt{D(D+4})-D}{2}\Leftrightarrow \\2C+D=\sqrt{D(D+4)}\Leftrightarrow \\4C^{2}+D^{2}+4CD=D^{2}+4D\Leftrightarrow \\C^{2}=D-CD$

Af grafen for C kan man se, at grænseværdien er C=1.

Da C for D>0 altid er mindre end 1, vil andet led altid være mindre end første led.
C² kan altså aldrig blive 1 eller mere.
Det samme må gælde for C.

Da C aldrig blir

Jeg er lidt forundret. Når du undersøger grafen for C, og ser at grænseværdien er 1, har du så ikke besvaret opgaven? Hvorfor så gå igennem de trin der leder dig til et udtryk for $C^2$ ?

Brugbart svar (0)

Svar #4
19. juli 2018 af StoreNord

Jeg regnede med, at opgaven skulle løses analytisk?

Svar #5
19. juli 2018 af Slashdash

#4
Jeg regnede med, at opgaven skulle løses analytisk?

Jeg ved ikke, hvordan den skulle løses. Min kommentar var ikke ment som at være provokerende. Det jeg mener er, at når du udleder:

"Da C for D>0 altid er mindre end 1, vil andet led altid være mindre end første led.
C² kan altså aldrig blive 1 eller mere.
Det samme må gælde for C."

Gør du det så ikke med udgangspunkt i grænseværdien (som du vel har udregnet vha. CAS), der fortæller dig, at når D går mod uendelig, så går C mod 1?

Brugbart svar (0)

Svar #6
19. juli 2018 af StoreNord

Jo.
Jeg udledte C² for at finde et pænere udtryk.
Og så tænkte jeg, at C vel opførte sig som C².
Men dèt med grænseværdien var svært for mig at fatte, indtil jeg så på grafen i Geogebra at C altid var mindre end 1.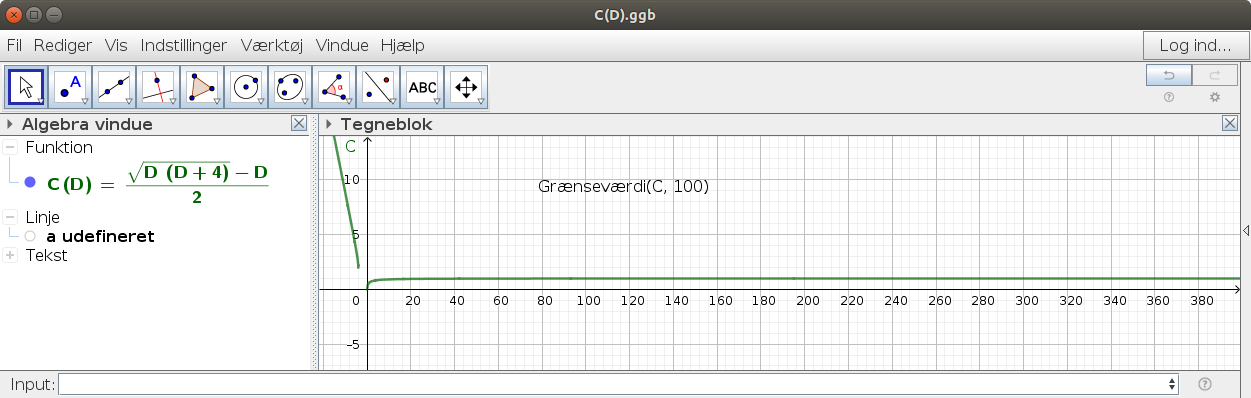 C(D).png

Vedhæftet fil:C(D).png

Brugbart svar (1)

Svar #7
19. juli 2018 af guuoo2

i 1) kan man forlænge brøken med og gang tælleren ud

$C=\frac {(\sqrt{D(D+4)}-D)(\sqrt{D(D+4)}+D)}{2(\sqrt{D(D+4)}+D)}=\frac{2 D}{\sqrt{D (D+4)}+D}$
C er større end
$\frac{2 D}{\sqrt{(D+4) (D+4)}+D}=\frac{D}{D+2}$

C er mindre end
$\frac{2 D}{\sqrt{D\cdot D}+D}=1$

I 2) divideres N(t) med M, hvormed f(t) ikke afhænger af M, men kun D, C og t.

De skal erstatte D og t og C med udtryk der kun afhænger af a, b, u og p.
Udtrykkene findes ved at løse tre ligninger (de to transformationsligninger samt udtrykket for C som funktion af D) mht. D, t og C.

Svar #8
24. juli 2018 af Slashdash

#7
i 1) kan man forlænge brøken med og gang tælleren ud

$C=\frac {(\sqrt{D(D+4)}-D)(\sqrt{D(D+4)}+D)}{2(\sqrt{D(D+4)}+D)}=\frac{2 D}{\sqrt{D (D+4)}+D}$
C er større end
$\frac{2 D}{\sqrt{(D+4) (D+4)}+D}=\frac{D}{D+2}$

C er mindre end
$\frac{2 D}{\sqrt{D\cdot D}+D}=1$

I 2) divideres N(t) med M, hvormed f(t) ikke afhænger af M, men kun D, C og t.

De skal erstatte D og t og C med udtryk der kun afhænger af a, b, u og p.
Udtrykkene findes ved at løse tre ligninger (de to transformationsligninger samt udtrykket for C som funktion af D) mht. D, t og C.

Mange tak. Ved du hvordan jeg kan løse opg. 3?

Skriv et svar til: Statistik og funktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.