Matematik

Sandsynlighed

31. oktober 2018 af JensAAAA (Slettet) - Niveau: Universitet/Videregående

Hej sp

Jeg sidder med denne opgave

Let X and Y be two independent Uniform (0,2) random variables, Find (PXY<1).

Jeg har forsøgt mig frem, men det volder problemer, når jeg prøver at skitser det. Jeg kan sagtens finde hele området (det er blot 1/(0+2), og dermed er koordinatetnerne til området (2,1/2), men hvordan finder jeg (PXY<1)?

En der kan hjælpe?

Brugbart svar (0)

Svar #1
31. oktober 2018 af swpply (Slettet)

Brugbart svar (0)

Svar #2
31. oktober 2018 af JendAAAA (Slettet)

Super, det giver bedre mening: Hvor får du 1/4 fra?

Brugbart svar (0)

Svar #3
31. oktober 2018 af JendAAAA (Slettet)

Kan jeg ikke blot sige, at indmaden i det første integrale er 2x?

Brugbart svar (0)

Svar #4
31. oktober 2018 af swpply (Slettet)

#2
Super, det giver bedre mening: Hvor får du 1/4 fra?

Det er normaliseringsfaktoren.

Brugbart svar (0)

Svar #5
31. oktober 2018 af swpply (Slettet)

#3
Kan jeg ikke blot sige, at indmaden i det første integrale er 2x?

Brug korrekt sprogbrug!!!

Hvis du med "indmaden i det første integrale" mener integraten, så nej. Integranten af de første integral er 2. Du har at

$\begin{align*} \frac{1}{4}\int_0^\frac{1}{2}2\,dx &= \frac{1}{4}\bigg(2\cdot\frac{1}{2}- 2\cdot0\bigg) \\ &= \frac{1}{4} \end{align*}$

$\begin{align*} \frac{1}{4}\int_\frac{1}{2}^2\frac{1}{x}\,dx &= \frac{1}{4}\Big(\ln(2) - \ln\big(\tfrac{1}{2}\big)\Big) \\ &= \frac{1}{4}\Big(\ln(2) + \ln(2)\Big) \\ &= \frac{1}{2}\ln(2) \\ &= \ln\big(2^\frac{1}{2}\big) \\ &= \ln\big(\sqrt{2}\big) \end{align*}$

Hvorfor at

$\text{Pr}(XY<1) = \frac{1}{4} + \ln\big(\sqrt{2}\big) \approx 59.657\;\%$

Brugbart svar (0)

Svar #6
31. oktober 2018 af JendAAAA (Slettet)

Brugbart svar (0)

Svar #7
31. oktober 2018 af jakob1325 (Slettet)

#5
#3
Kan jeg ikke blot sige, at indmaden i det første integrale er 2x?

Brug korrekt sprogbrug!!!

Hvis du med "indmaden i det første integrale" mener integraten, så nej. Integranten af de første integral er 2. Du har at

$\begin{align*} \frac{1}{4}\int_0^\frac{1}{2}2\,dx &= \frac{1}{4}\bigg(2\cdot\frac{1}{2}- 2\cdot0\bigg) \\ &= \frac{1}{4} \end{align*}$

og

$\begin{align*} \frac{1}{4}\int_\frac{1}{2}^2\frac{1}{x}\,dx &= \frac{1}{4}\Big(\ln(2) - \ln\big(\tfrac{1}{2}\big)\Big) \\ &= \frac{1}{4}\Big(\ln(2) + \ln(2)\Big) \\ &= \frac{1}{2}\ln(2) \\ &= \ln\big(2^\frac{1}{2}\big) \\ &= \ln\big(\sqrt{2}\big) \end{align*}$

Hvorfor at

$\text{Pr}(XY<1) = \frac{1}{4} + \ln\big(\sqrt{2}\big) \approx 59.657\;\%$

Det er altså ikke korrekt det du skriver. Nu vil jeg ikke give hele løsningen, da det er en obligatorisk opgave på universitetet, men svaret ender med at give: $\frac{1}{2}*(1+\ln(2)))\approx 0.85$

Brugbart svar (0)

Svar #8
31. oktober 2018 af swpply (Slettet)

#7 Jeg er med på at du ikke ønsker at gennemgå besvarelsen af opgaven nu hvor den er en obligatorisk opgave i kursus. Men hvis du fejlagtig ytre påstanden at

$(1)\qquad\qquad\qquad\qquad\qquad\text{Pr}(XY<1) = \frac{1}{2}\cdot\bigg(\frac{1}{2} + \ln(2)\bigg)$

ikke er det korrekte svar til opgaven, så bør du påpege præcist hvor fejlen min udregning er. Jeg er desvære bange for at et sådant forsøg vil vise sig at være umuligt for dig –– idet at (1) er sand, hvilket du også hurtigt vil blive bekræftet i hvis du laver en hurtig numerisk simulation heraf

Vedhæftet fil:swpply.png

Brugbart svar (0)

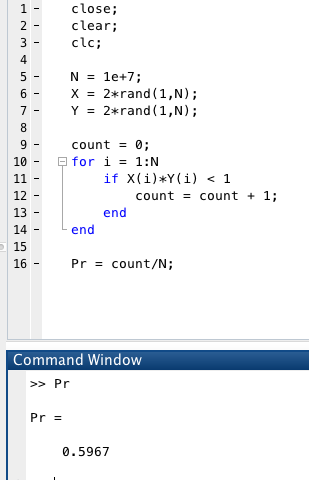
Svar #9
06. november 2018 af helpn

#4
#2
Super, det giver bedre mening: Hvor får du 1/4 fra?

Det er normaliseringsfaktoren.

Hej! Først og fremmest tusind tak for nogle brugbare svar. Forstår dog ikke hvor de 1/4 kommer fra. Kan se du skriver at det er jf. normaliseringsfaktoren, men det har jeg aldrig hørt om. Kan du måske uddybe det, forklare hvordan du finder frem til det? På forhånd tak

Brugbart svar (0)

Svar #10
06. november 2018 af oppenede

(X, Y) har support på [0,2]×[0,2], hvilket er et kvadrat med areal 4.

Sandsynligheden for hændelsen P(XY < 1) er arealet af området hvor hændelsen indtræffer (vist i #1) divideret med arealet af supporten for (X, Y), som er 4.

Sandsynligheden kan kun bestemmes på den måde, når (X, Y) er uniformt fordelt over sin support.

Skriv et svar til: Sandsynlighed

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.