Lige nu 125 online.

Persondatapolitik

Matematik

Cosinus og Sinus relationer

06. december 2018 af ISwallowYoPapa - Niveau: B-niveau

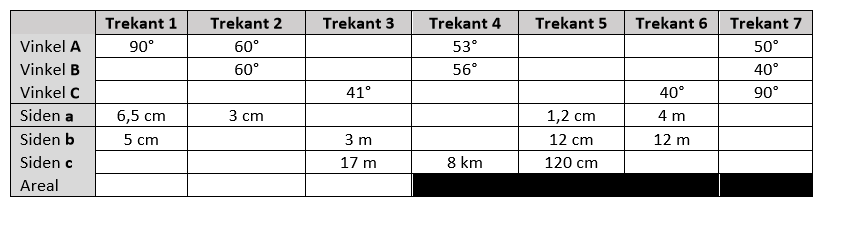
Jeg har virkelig brug for at blive hjulpet til denne opgave da jeg slet ikke forstår den

Vedhæftet fil: heehee.PNG

Brugbart svar (1)

Svar #1
06. december 2018 af mathon

Brugbart svar (1)

Svar #2
06. december 2018 af mathon

$\small \textup{Trekant 1:}$
$\small c=\sqrt{6.5^2-5^2}=4.15$

$\small \sin(B)=\frac{5}{6.5}$

$\small B=\sin^{-1}\left (\frac{5}{6.5} \right )=50.3\degree$

$\small C=90\degree-50.3\degree=39.7\degree$

areal:
$\small T=\tfrac{1}{2}\cdot c\cdot b=\tfrac{1}{2}\cdot 4.15\cdot 5=10.38$

Brugbart svar (1)

Svar #3
06. december 2018 af mathon

$\small \small \textup{Trekant 2:}$
$\small b=c=a=3\; cm$

$\small C=B=A=60\degree$

areal:
$\small T=\tfrac{1}{2}\cdot b\cdot \sin(A)\cdot c=\tfrac{1}{2}\cdot(3\; cm)\cdot \tfrac{\sqrt{3}}{2}\cdot (3 \;cm )=\frac{\sqrt{3}}{4}\cdot (3\; cm)^2$

Brugbart svar (1)

Svar #4
06. december 2018 af mathon

$\small \small \small \textup{Trekant 5:}$
$\small A=\cos\left ( \frac{b^2+c^2-a^2}{2\cdot b\cdot c} \right )$

$\small B=\cos\left ( \frac{a^2+c^2-b^2}{2\cdot a\cdot c} \right )$

$\small C=\cos\left ( \frac{a^2+b^2-c^2}{2\cdot a\cdot b} \right )$

Brugbart svar (0)

Svar #5
06. december 2018 af mathon

$\small \small \small \textup{Trekant 3:}$
$\small \frac{\sin(B)}{3}=\frac{\sin(41\degree)}{17}$

$\small B=\sin^{-1}\left(3\cdot \frac{\sin(41\degree)}{17}\right)=6.6\degree$

$\small \frac{a}{\sin(41\degree+6.6\degree)}=\frac{17}{\sin(41\degree)}$

$\small a=\sin(41\degree+6.6\degree)\cdot \frac{17}{\sin(41\degree)}=19.1$

$\small T=\tfrac{1}{2}\cdot a\cdot b\cdot \sin(C)=\tfrac{1}{2}\cdot 19.1\cdot 3\cdot \sin(41\degree)$

$\small A=180\degree-(41\degree+6.6\degree)=132.4\degree$

Brugbart svar (0)

Svar #6
07. december 2018 af mathon

$\small \small \small \small \textup{Trekant 7:}$
   $\small a=c\cdot \cos(40\degree)$
   $\small c\in\mathbb{R}_+$
   $\small b=c\cdot \sin(40\degree)$

Skriv et svar til: Cosinus og Sinus relationer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.

Seneste indlæg
A: Differentation (2)
A: Integral arealberegning for punk... (5)
9: Prøveoplæg til fordybelsesområde... (1)
Biostatistik og Epidemiologi i m... (0)
9: Jorden og Livets udvikling (0)

Populære indlæg
A: Differentation (2)
A: Integral arealberegning for punk... (5)
9: Levende reklamer (3)
9: hvorfor er kobber giftigt og sta... (4)
9: Prøveoplæg til fordybelsesområde... (1)

Om Studieportalen.dk: Om Studieportalen.dk | Kontakt | Annoncering | Studiebladet | Ophavsret | Cookie- og persondatapolitik

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se