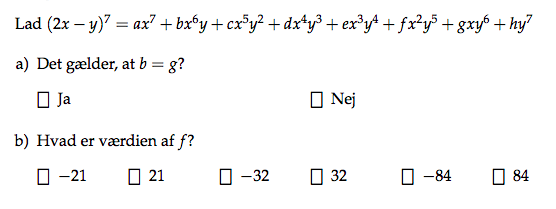Matematik

Pascals trekant

21. februar 2019 af Warrio - Niveau: Universitet/Videregående

Hej

Jeg har vedhæftet opgaven som et billede. I opgave a) er b ≠ g, da b vil være positiv og g er negativ, ikke sandt?

I opgave b), for at bestemme, hvad f er, kan man aflæse det vha. pascals trekant, hvis jeg husker rigtigt. Og hvis ja, kan jeg få hjælp til, hvordan det nu var man kunne aflæse det.

På forhånd tak!

Vedhæftet fil: Screen Shot 2019-02-21 at 15.52.23.png

Brugbart svar (0)

Svar #1
21. februar 2019 af mathon

Brugbart svar (0)

Svar #2
21. februar 2019 af mathon

a)
Nej

Brugbart svar (0)

Svar #3
21. februar 2019 af AMelev

Koefficienterne {a,b,c,d,e,f,g,h} = {k(7,0),k(7,1),k(7,2),k(7,3),k(7,4),k(7,5),k(7,6),k(7,7)} eller med Pascals trekant {1,7,21,35,35,21,7,1}

Nu kan du selv, ikke?

Svar #4
21. februar 2019 af Warrio

er f så -21? det svarede jeg nemlig, men det er forkert. det siger at f = -84 :/

Brugbart svar (0)

Svar #5
21. februar 2019 af Soeffi

#1. Man har:

$(a+b)^7= \sum_{i=0}^{7}\binom{7}{i}\cdot a^{7-i}\cdot b^i$

Man skal finde det sjette led (i = 5), når a = 2x og b = -y. Man får:

$\binom{7}{5}\cdot (2x)^2\cdot (-y)^5= -21\cdot 4\cdot x^2 y^5=-84 x^2 y^5$

Brugbart svar (0)

Svar #6
21. februar 2019 af AMelev

#4 Undskyld. Jeg havde overset, at der stod (2x - y) og ikke (x + y).
Se #5

Skriv et svar til: Pascals trekant

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.