Matematik

En funktion med punktmængde

28. februar 2019 af Holmo123 - Niveau: B-niveau

En funktion er bestemt ved

f(x)=-x²+3,5*x+kvadratroden af x, x≥0

Grafen for f afgrænser i første kvadrant sammen med første aksen en punktmængde M, der har et areal

Tegn grafen for f og bestemt arealet af M

Noget der ved hvordan man gør det ?

Brugbart svar (0)

Svar #1
28. februar 2019 af ringstedLC

Beregn f(x) = 0. Det er så integrationsgrænserne for F(x).

Brugbart svar (0)

Svar #2
28. februar 2019 af AMelev

Tegn grafen først - så kan du måske selv komme videre.

Brug dit CAS-værktøj til at bestemme arealet - det kan måske også lede dig på sporet - og så har du i hvert fald en kontrol.

Svar #3
28. februar 2019 af Holmo123

Får det til 4

Hvad betyder det så ?

Brugbart svar (0)

Svar #4
28. februar 2019 af OliverHviid

Jamen så betyder det jo, at den punktmængde M, som grafen for f afgrænser i første kvadrant sammen med førsteaksen, har et areal på 4.

Brugbart svar (0)

Svar #5
28. februar 2019 af ringstedLC

Forkert. Kan du vedhæfte et billede af udregningen.

Brugbart svar (0)

Svar #6
28. februar 2019 af AMelev

#3 Hvad er det, du får til 4?

Hvad får du nulpunkterne til?

Brugbart svar (0)

Svar #7
28. februar 2019 af OliverHviid

Som ringsted og AMelev nævner: kom lige med alle udregningerne, så er det lettere at se, hvor du har regnet forkert.

Svar #8
01. marts 2019 af Holmo123

Jeg har bare sat funktion lig nul og brugt solve til at regne det. Så får jeg at x er = 4 eller x= 0

Brugbart svar (0)

Svar #9
01. marts 2019 af OliverHviid

Ja, integrationsgrænserne er x=0 (den nedre grænse) og x=4 (den øvre), men det er jo ikke arealet.

Brugbart svar (0)

Svar #10
01. marts 2019 af AMelev

Jeg er lidt forvirret.
Din profil angiver Stx 2g og spørgsmålet er angivet som B-niveau, men Integralregning indgår, så vidt jeg kan læse, ikke som kernestof i B-niveau efter ny ordning. Er det et supplerende emne, eller...?

For arealberegningen se evt. dette link.

Brugbart svar (0)

Svar #11
01. marts 2019 af OliverHviid

Nu spørger jeg lige af ren og skær nysgærrighed: er integralregning så A-niveau-stof efter den nye ordning? Det virker da lidt underligt at fjerne det fra B-niveauet, hvis du spørger mig.

Svar #12
02. marts 2019 af Holmo123

Har ingen ide. Jeg bed bare at det er i min opgave som er på b niveau

Brugbart svar (0)

Svar #13
02. marts 2019 af AMelev

#11 Vektorregning er kommet ind allerede på C-niveu, så noget måtte jo så skubbes til B-niveau og videre til A-niveau. Rumgeometri er helt ude, til gengæld er vektorfunktioner kommet ind i varmen igen på A. chi²-test er skiftet tilbage til binomialtest og residualerne har fået en fremtrædende plads. Det er vist de vigtigste ændringer - bortset fra eksamensformen.

Ovenstående gælder Stx og Hf, jeg har ikke gransket undervisningsvejledningerne for Htx og Hhx.

Brugbart svar (0)

Svar #14
02. marts 2019 af OliverHviid

#13 tak for svaret.

Brugbart svar (0)

Svar #15
02. marts 2019 af ringstedLC

Arealet mellem grafen for en funktion og fx x-aksen beregnes ved at integrere funktionen og beregne det bestemte integrale.

Ex.:

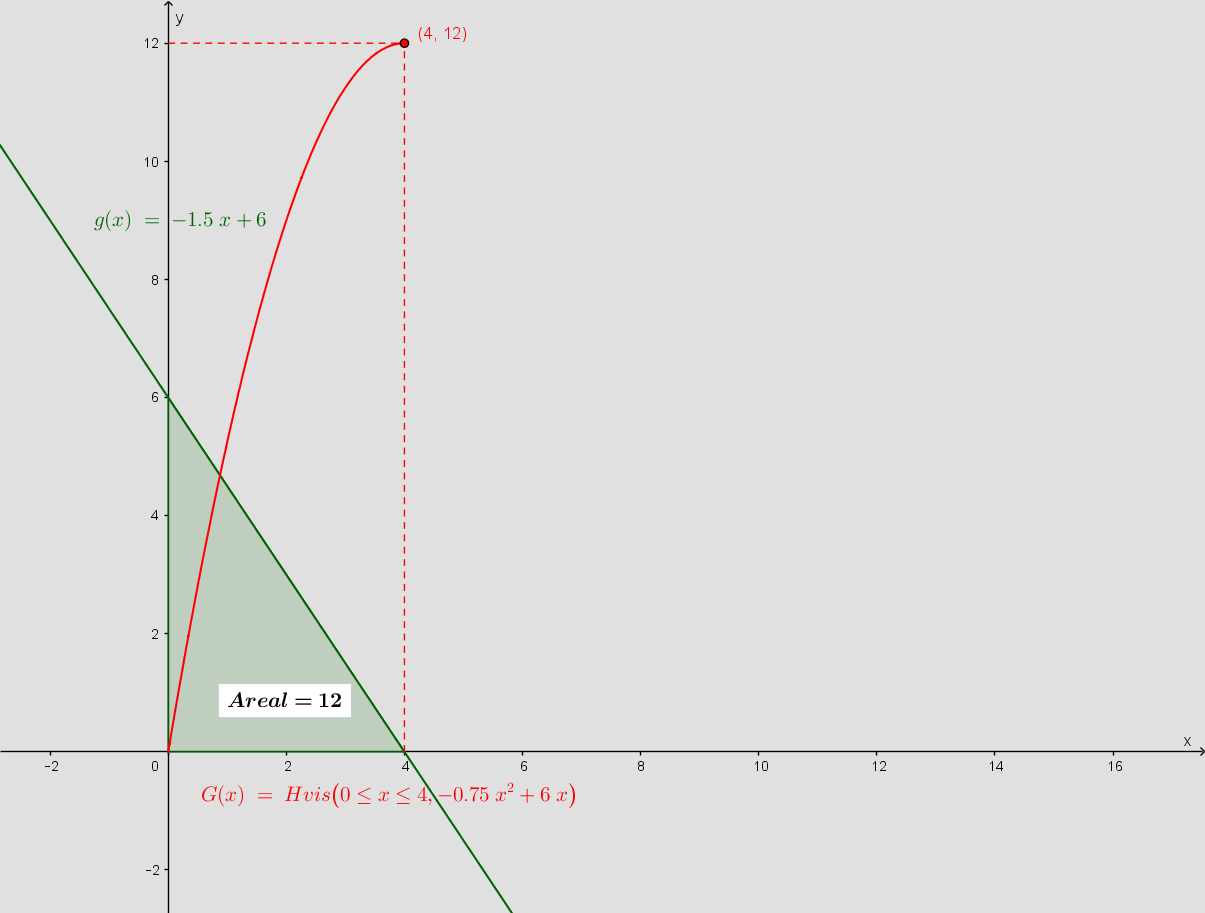
$\begin{align*} Areal_T &= 0.5\cdot h\cdot g \\ &= 0.5\cdot 6\cdot 4=12 \\ Areal_T &= \int_{{\color{Red} 0}}^{{\color{Blue} 4}}{g(x)\;dx} \\ &= \int_{{\color{Red} 0}}^{{\color{Blue} 4}}{-1.5x+6\;dx} = \int_{{\color{Red} 0}}^{{\color{Blue} 4}}{-1.5x^{\color{DarkGreen} 1}+6x^{\color{Magenta} 0}\;dx} \\ &=\left [ \tfrac{-1.5}{{\color{DarkGreen} 1}+1}x^{{\color{DarkGreen} 1}+1} +\tfrac{6}{{\color{Magenta} 0}+1}x^{{\color{Magenta} 0}+1} \right ]_{{\color{Red} 0}}^{{\color{Blue} 4}} =\left [ -0.75x^2+6x \right ]_{{\color{Red} 0}}^{{\color{Blue} 4}} \\\\ &=\left ( -0.75\cdot {\color{Blue} 4}^2+6\cdot {\color{Blue} 4} \right ) -\left ( -0.75\cdot {\color{Red} 0}^2+6\cdot {\color{Red} 0} \right ) \\ Areal_T &= 12 \end{align*}$

Når det bestemte integrales interval er 0 til x₀ er arealet G(x₀).

Vedhæftet fil:B_M_073_1 - Punktmængde, int._Holmo123.png

Brugbart svar (0)

Svar #16
02. marts 2019 af ringstedLC

Det er altid en god ide at tegne og her forlanges det.

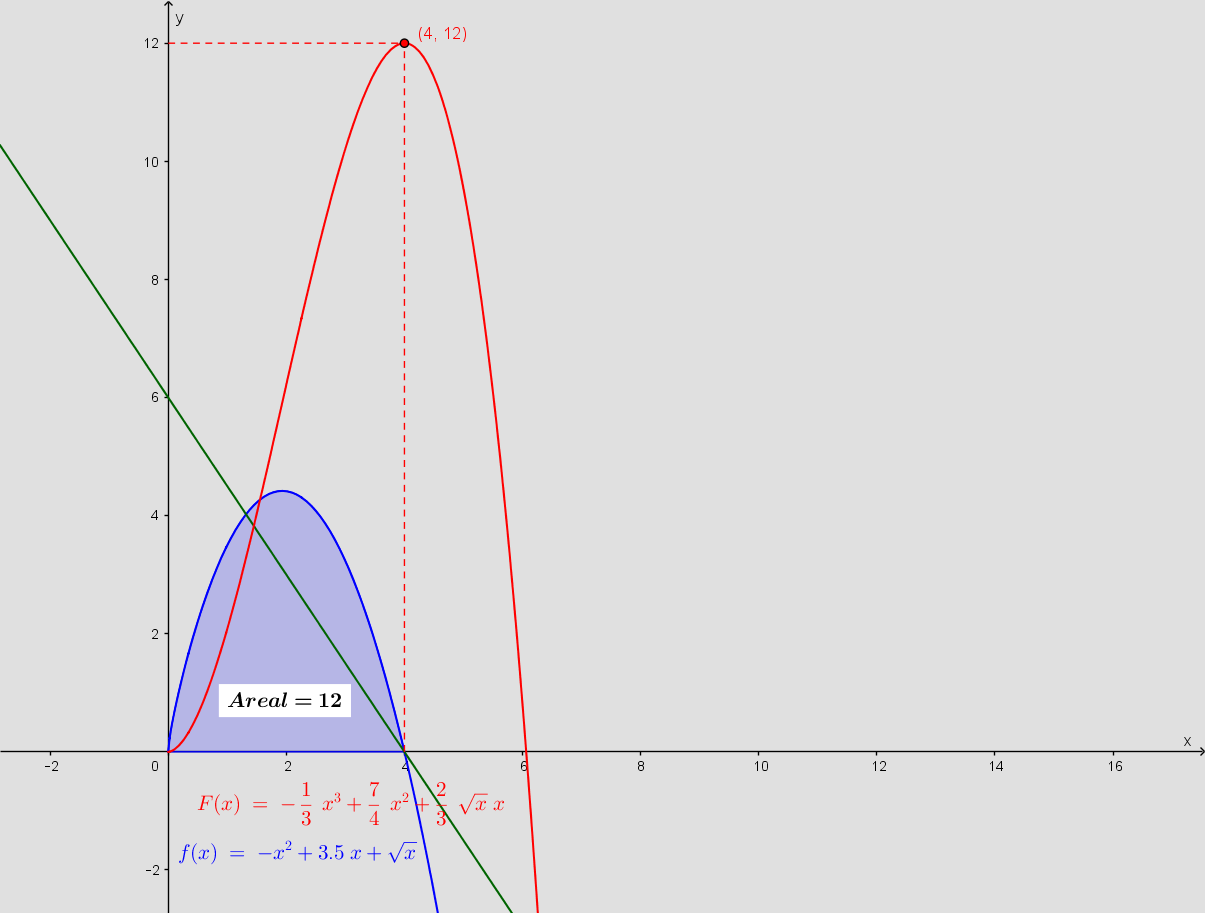
$\begin{align*} f(x) &= 0\Rightarrow x={\color{Red} 0}\vee x={\color{Blue} 4}\Downarrow \\ Areal_M &= \int_{{\color{Red} 0}}^{{\color{Blue} 4}}{-x^2+3.5x+\sqrt{x}\;dx} \\ &= \int_{{\color{Red} 0}}^{{\color{Blue} 4}}{-x^{\color{DarkGreen} 2}+3.5x^{\color{Magenta} 1}+x^{{\color{Cyan} 0.5}}\;dx} \\ &= \left [ \tfrac{-1}{{\color{DarkGreen} 2}+1}x^{{\color{DarkGreen} 2}+1} +\tfrac{3.5}{{\color{Magenta} 1}+1}x^{{\color{Magenta} 1}+1} +\tfrac{1}{{\color{Cyan} 0.5}+1}x^{{\color{Cyan} 0.5}+1} \right ]_{{\color{Red} 0}}^{{\color{Blue} 4}} =\left [ -\tfrac{1}{3}x^3+\tfrac{3.5}{2}x^2+\tfrac{1}{1.5}x^{1.5} \right ]_{{\color{Red} 0}}^{{\color{Blue} 4}} \\\\ &= \left ( -\tfrac{1}{3}\cdot {\color{Blue} 4}^3+\tfrac{3.5}{2}\cdot {\color{Blue} 4}^2+\tfrac{1}{1.5}\cdot {\color{Blue} 4}^{1.5} \right ) - \left ( -\tfrac{1}{3}\cdot {\color{Red} 0}^3+\tfrac{3.5}{2}\cdot {\color{Red} 0}^2+\tfrac{1}{1.5}\cdot {\color{Red} 0}^{1.5} \right ) \\ Areal_M &= 12 \end{align*}$

Vedhæftet fil:B_M_073_2 - Punktmængde, int._Holmo123.png

Skriv et svar til: En funktion med punktmængde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.