Matematik

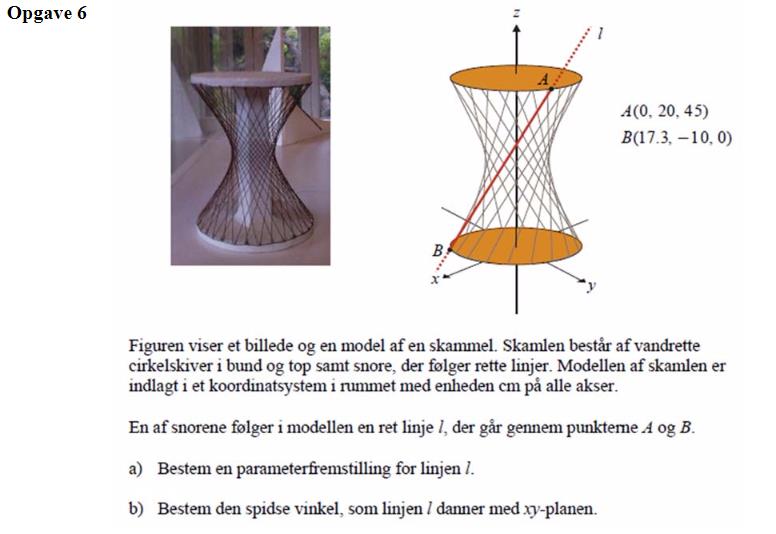
Vektor 3D

10. marts 2019 af mi28 - Niveau: A-niveau

hej jeg har en opgave her, der er lidt svært.

jeg har fået svaret i opgave a. er der nogen der kan hjælpe mig på opgave b?

Vedhæftet fil: m.jpg

Brugbart svar (0)

Svar #1
10. marts 2019 af janhaa

$\vec{AB}=[17.3,-30,-45]\\ \\ (x,y,z)=[17.3,-30,-45]\*t+(0,20,45)$

Brugbart svar (0)

Svar #2
10. marts 2019 af oppenede

Find vinklen mellem retningsvektoren for linjen og vektoren (0,0,1), dvs. vinklen som linjen danner med z-aksen. 90 minus den vinkel giver vinklen som dannes med xy-planet.

Brugbart svar (0)

Svar #3
10. marts 2019 af ringstedLC

b) Vinklen findes mellem vektor AB og fx -stedvektor (B).

Brugbart svar (0)

Svar #4
11. marts 2019 af mathon

Brugbart svar (1)

Svar #5
11. marts 2019 af mathon

b)
eller 90° minus den spidse vinkel mellem xy-planens normalvektor $\small \overrightarrow{k}=\begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}$ og $\small \overrightarrow{BA}=\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}$

$\small 90\degree-\cos^{-1}\left ( \frac{\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}\cdot \begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}}{56.7828} \right )=90\degree-\cos^{-1}\left ( 0.79249 \right )=90\degree-37.58\degree=52.4\degree$

Svar #6
13. marts 2019 af mi28

#5
b)
eller 90° minus den spidse vinkel mellem xy-planens normalvektor $\small \overrightarrow{k}=\begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}$ og $\small \overrightarrow{BA}=\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}$

$\small 90\degree-\cos^{-1}\left ( \frac{\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}\cdot \begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}}{56.7828} \right )=90\degree-\cos^{-1}\left ( 0.79249 \right )=90\degree-37.58\degree=52.4\degree$

hej Mathon, skal det ikke være $AB=(17,5;-30; -45)$ ?

Brugbart svar (0)

Svar #7
13. marts 2019 af janhaa

#6
#5
b)
eller 90° minus den spidse vinkel mellem xy-planens normalvektor $\small \overrightarrow{k}=\begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}$ og $\small \overrightarrow{BA}=\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}$

$\small 90\degree-\cos^{-1}\left ( \frac{\begin{pmatrix} -17.3\\30 \\ 45 \end{pmatrix}\cdot \begin{pmatrix} 0\\0 \\ 1 \end{pmatrix}}{56.7828} \right )=90\degree-\cos^{-1}\left ( 0.79249 \right )=90\degree-37.58\degree=52.4\degree$

hej Mathon, skal det ikke være $AB=(17,5;-30; -45)$ ?

Skriv et svar til: Vektor 3D

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.