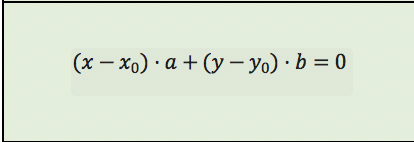Matematik

Forklaring af ligning

25. marts 2019 af TGGYM - Niveau: B-niveau

Nogen der kan hjælpe med en forklarende tekst til den her ligning?

Vedhæftet fil: Skærmbillede 2019-03-25 kl. 13.05.33.png

Brugbart svar (0)

Svar #1
25. marts 2019 af mathon

Brugbart svar (0)

Svar #2
25. marts 2019 af mathon

Den rette linje $\small l$ gennem P_o(x_o,y_o) med normalvektor $\small \overrightarrow{n}=\bigl(\begin{smallmatrix} a\\b \end{smallmatrix}\bigr)$
har ligningen:

$\small l\textup{:}\quad\begin{pmatrix} a\\b \end{pmatrix}=\begin{pmatrix} x-x_o\\y-y_o \end{pmatrix}=0$

$\small l\textup{:}\quad a\cdot (x-x_o)+b\cdot (y-y_o)=0$

Brugbart svar (0)

Svar #3
25. marts 2019 af AMelev

Det ligner ligningen for en retlinje gennem punktet (x₀,y₀) og med normalvektor $\vec n=\binom{a}{b}$ .

Hvad er det, du er på jagt efter? Er det udledningen?

Brugbart svar (0)

Svar #4
25. marts 2019 af PeterValberg

Prøv at se video nr. 21 og 22 på denne videoliste < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #5
25. marts 2019 af AMelev

Tastefejl i #2. Det første = skulle være ·, da det er skalarproduktet, der er 0, idet de to vektorer er ortogonale.

Se evt. dette link. Scrol ned til "Hvorfor ser ligningen sådan ud?".
NB! Der er fejl i videolektionen.

Brugbart svar (0)

Svar #6
25. marts 2019 af mathon

Korrektion af tastefejl:

Den rette linje $\small l$ gennem P_o(x_o,y_o) med normalvektor $\small \overrightarrow{n}=\bigl(\begin{smallmatrix} a\\b \end{smallmatrix}\bigr)$
har ligningen:

$\small \small l\textup{:}\quad\begin{pmatrix} a\\b \end{pmatrix}\cdot \begin{pmatrix} x-x_o\\y-y_o \end{pmatrix}=0$

$\small l\textup{:}\quad a\cdot (x-x_o)+b\cdot (y-y_o)=0$

Svar #7
25. marts 2019 af TGGYM

Mange tak for hjælpen guys, opgaven gik bare ud på at forklare ligningen.

Skriv et svar til: Forklaring af ligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.