Matematik
Parametrisering af trekant
Hej SP, jeg sidder og skal til reeksamen i matematik 1 her til august, og én af mine store udfordringer er parametriseringer.
Jeg sidder og laver det eksamenssæt som besejrede mig, og jeg uploader løsningsforslaget som billede da jeg ikke forstår løsningen (som virker ret simpel).
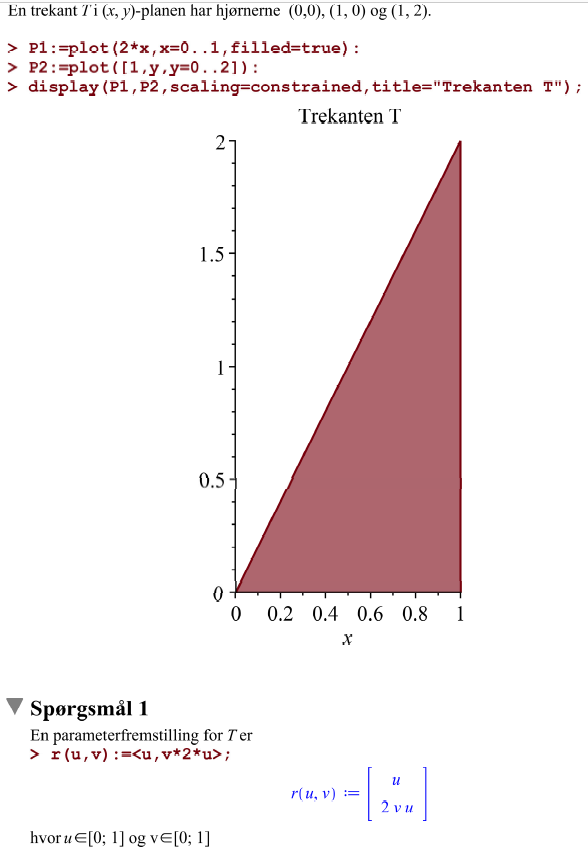
Jeg har fået opgaven: En trekant T i (x,y)-planen har hjørnerne (0,0) (1,0) og (1,2) - angiv en parameterfremstilling for T:
Og løsningsforslaget siger således men jeg forstår ikke hvordan man kommer frem til det?:
Svar #1
10. juli 2019 af Soeffi
#0. Du kan vel se sådan på det, at r(u,v) = (u, 2u) er linjestykket fra (0,0) til (1,2). Du skal så bruge det der ligger under dette linjestykke og til det bruger du v, som du ganger med 2u.
Lad os sige, at du skulle parameterisere området under kurven: y = x2. Dette kunne så gøres ved: r(u,v) = (u,v·u2).
Svar #2
10. juli 2019 af TeamFinal
TUSIND TAK! Nøj, dejligt simpelt forklaret - jeg tror forvirringen hos mig er kommet af at jeg ikke kunne plotte parametriseringen, og at jeg havde set en meget besværlig måde at lave parametrisering på.
kan dette også være rigtig?:
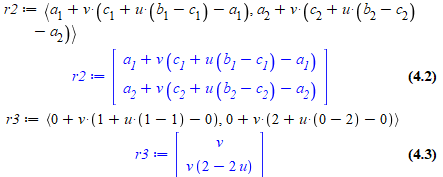
Svar #3
10. juli 2019 af TeamFinal
det her er den formel jeg er gået ud fra , og så bare i R2 i stedet

Svar #4
10. juli 2019 af Soeffi
#3. Den generelle trekant.
Mit gæt er: Tag trekant ABC og lav parallelogram ABA'C. Dette parallelogram må have parameteriseringen:
(x,y) = t·AB + s·AC, t ∈[0;1] og s∈[0;1].
Trekant ABC kan så tænkes at have parameteriseringen:
(x,y) = t·AB + s·AC, t ∈[0;1] og s∈[0;1-t].
Skriv et svar til: Parametrisering af trekant
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


