Matematik

Sinus og Cosinus i en graf

02. september 2019 af Mads256 - Niveau: A-niveau

Okay så jeg har denne opgave, men ved ikke helt hvordan jeg skal formulere mig i min besvarelse, opgaven er:

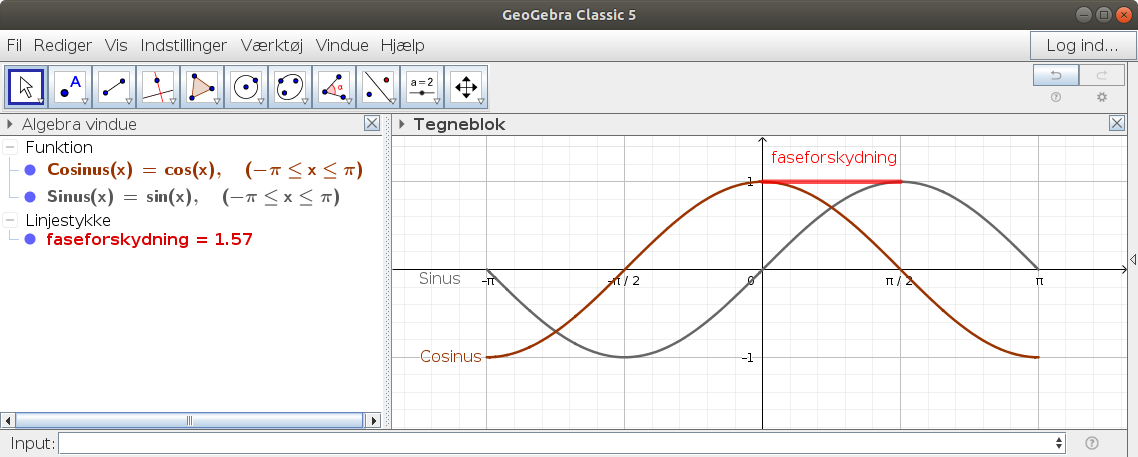
"Optegn sinus og cosinus
funktionerne i samme koordinatsystem. Kommentér graferne.
Hvad er sammenhæng en mellem de to grafer?
Kom herunder ind på den såkaldte faseforskydning mellem de to funktioner."

Altså jeg ved ikke om man bare skal sige at de er en, mens bare ½π fra hinanden på x-aksen? Aner ikke hvad de mener med sammenhæng her, og så har vores lærer heller ikke gået ordenligt igennem hvad faseforskydning er... Så jeg er lidt lost her :/

Brugbart svar (1)

Svar #1
02. september 2019 af mathon

$\small \small \begin{array}{lllll} \cos\left (x -\frac{\pi }{2} \right )=\sin(x)&&\cos-\textup{grafen parallelforskudt efter }\begin{pmatrix} \frac{\pi }{2}\\0 \end{pmatrix}\\\\ \sin\left ( x+\frac{\pi }{2} \right )=\cos(x)&&\sin-\textup{grafen parallelforskudt efter }\begin{pmatrix} -\frac{\pi }{2}\\0 \end{pmatrix} \end{array}$

Svar #2
02. september 2019 af Mads256

Tusind tak, du er en livredder haha

Brugbart svar (0)

Svar #3
02. september 2019 af StoreNord

Ups!

Brugbart svar (1)

Svar #4
02. september 2019 af StoreNord

Skærmbillede fra 2019-09-02 22-40-20.png

Vedhæftet fil:Skærmbillede fra 2019-09-02 22-40-20.png

Brugbart svar (1)

Svar #5
02. september 2019 af ringstedLC

Faseforskydning er netop den forskel på ½ π som du har bemærket. Du har måske i fysik om bølger hørt om begreberne medfase og modfase. To bølger i medfase adderes fordi deres udsving er sammenfaldende til en bestemt "tid". To bølger i modfase er faseforskudt med π (180º) og skal subtraheres fordi deres udsving er modsat hinanden til en bestemt "tid". Sinus og cosinus er hverken i med- eller modfase med hinanden, men er forskudt med en værdi mellem 0 og π, nemlig ½ π.

Med "tid" menes periodetid fordi sinus og cosinus er periodiske funktioner. De gentager sig selv efter et omløb i enhedscirklen (se/husk på definitionen af sinus/cosinus).

Værdien ½ π (90º) er radianer som er et andet mål for grader af den vinkel som dannes mellem et linjestykke fra et punkt på enhedscirklen til centrum, og x-aksen. ½ π er længden af buestykket fra (1,0) til (0,1). Så i dit koordinatsystem er det buestykke rettet ud til en ret linje, der er sammenfaldende med x-aksen. Eksempler på sammenhænge:

$\begin{align*} \sin(0)=\sin(0^{\circ}) &= 0\;,\;\cos\left (0 \right )=\cos(0^{\circ})=1 \\ \sin(\pi)=\sin(180^{\circ}) &= 0\;,\;\cos\left (\pi \right )=\cos(90^{\circ})=0 \\ \sin(2\pi)=\sin(360^{\circ}) &= 0\;,\;\cos\left (2\pi \right )=\cos(360^{\circ})=1 \\\\ \sin\left (\tfrac{\pi}{2} \right )=\sin(90^{\circ}) &= 1=\cos(0)=\cos(0^{\circ}) \\ \cos\left (\tfrac{\pi}{2} \right )=\cos(90^{\circ}) &= 0=\sin(0)=\sin(0^{\circ}) \\ \cos\left (\pi \right )=\cos(180^{\circ}) &= -1=\sin\left (\tfrac{3\pi}{2} \right )=\sin(270^{\circ}) \\ \sin(45^{\circ})=\sin\left ( \tfrac{\pi}{4} \right )=\cos\left ( \tfrac{\pi}{4} \right ) &= \tfrac{\sqrt{2}}{2} \\ \left (\sin\left ( \tfrac{\pi}{4} \right ) \right )^2 +\left (\cos\left ( \tfrac{\pi}{4} \right ) \right )^2 &= 1^2 \text{ (Pythagoras)} \\ \end{align*}$

Skriv et svar til: Sinus og Cosinus i en graf

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.