Fysik
Usikkerheder ved mindste og største forhold
Hej.
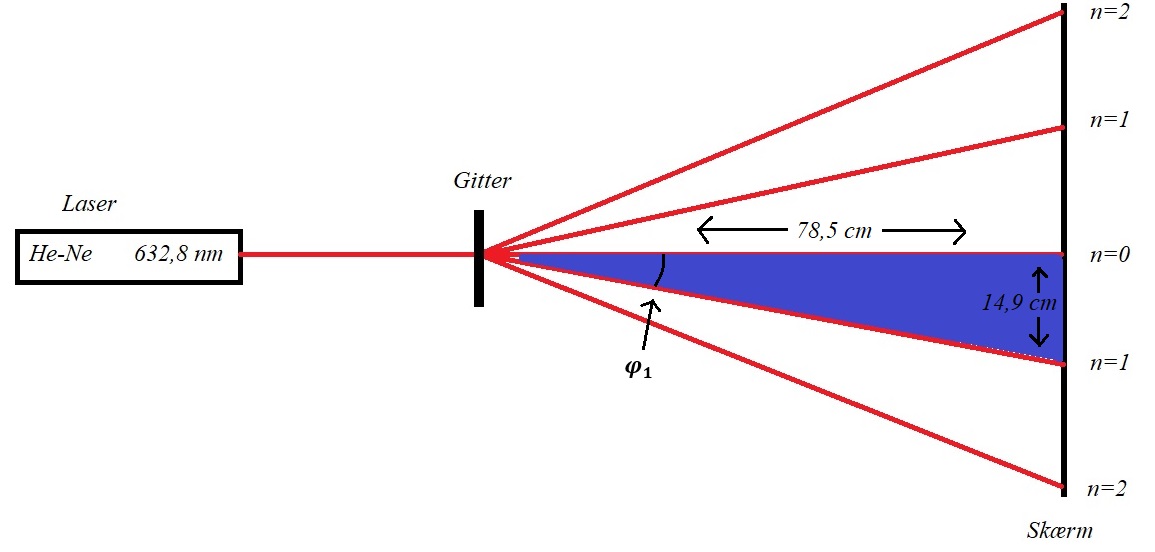
Jeg sidder og laver nogle fysik opgaver og har læst grundigt igennem første del af modulet som handler om bølger, lys og farver. Opgaverne indtil videre har handlet om beregning af gitterkonstanten og afbøjningsvinklen af en laserstråle gennem et gitter. Nu kommer jeg dog til et af spørgsmålene som siger:
-
"Der er kun to målinger i vores forsøg: Målingen af længden mellem pletterne og målingen af længden
mellem gitteret og skærmen. Vi vurderer at målingen af
er bestemt plus/minus 0,2 cm mens at usikkerheden på
kun er bestemt plus/minus 0,5 cm.
En brøk er mindst mulig når tælleren er mindst mulig OG nævneren er størst mulig og en brøk er størst mulig når tælleren er størst mulig OG nævneren er mindst mulig.
Brug dette samme med de nævnte usikkerheder til at vise, at det betyder, at det mindste forhold mellem og
er
, samt at det største forhold mallem
og
er lig med
".
-
Der har på intet tidspunkt i materialet, vi har skullet studere, været snak om hvordan vi ville kunne løse sådan en problemstilling. Jeg har intet held haft med at finde hjælp på nettet eller youtube, så jeg håber på at der er nogle af jer der kan give mig en hjælpende hånd.
På forhånd tak :-)
Svar #2
15. november 2019 af peter lind
Du kan i princippet godt gøre som foreslået; men så får du de største afvigelser, og det er alså ikke det der bedes om. Det er jo højst usandsynmligt at målingerne arbejder sammen om at give et yderligtgående resultat.
de normale måde er at se på den relative sandsynlighed ved at bruge formlen kvrod( (Δl1/l1)2 + (Δl2/l2)2)
Svar #3
15. november 2019 af ringstedLC
Der er ikke unormalt i at du ved et fysikforsøg skal nævne fejlkilder og usikkerheder. Her skal usikkerhederne så også beregnes:
hvilket så betyder:
Skriv et svar til: Usikkerheder ved mindste og største forhold
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.