Matematik

funktion og ligning

19. januar 2020 af mikkel981 - Niveau: B-niveau

Hej.

Hvordan løses disse to opgaver? Det er uden hjælpemidler.

Vedhæftet fil: opgave.png

Brugbart svar (0)

Svar #1
19. januar 2020 af Capion1

Størrelsen indenfor numerisksymbolet deles op for negativ og for positiv og nul.

Svar #2
19. januar 2020 af mikkel981

Det forstår jeg ikke helt

Brugbart svar (0)

Svar #3
19. januar 2020 af Capion1

|x - 2| = x - 2 for x ≥ 2
|x - 2| = - x + 2 for x < 2

Brugbart svar (0)

Svar #4
19. januar 2020 af ringstedLC

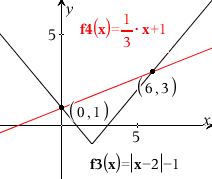
a) Grafen er stykkevis lineær pga. den numeriske værdi.

$\begin{align*} |x-2| &\geq 0 \Rightarrow x-2\geq 0\Rightarrow x\geq \;? \\ |x-2| &<0\Rightarrow \;? \end{align*}$

Se mere i eksempel 1 på https://www.webmatematik.dk/lektioner/matematik-c/ligninger/numeriske-ligninger

b) På baggrund af forholdene i a) kan venstresiden deles op i to lineære grafer. Derved kan ligningen løses som to gange skæringen mellem to linjer.

Brugbart svar (0)

Svar #5
20. januar 2020 af mathon

og dermed:

$\small f(x)=\left\{\begin{array}{lll}x-3&\textup{for }x\geq 2\\-x+1&\textup{for }x< 2 \end{array}\right.$

Brugbart svar (0)

Svar #6
20. januar 2020 af mathon

$\small \small \begin{array}{llll} &f(x)=\frac{1}{3}x+1&\textup{for }x\geq 2\\\\&x-3=\frac{1}{3}x+1\\\\&\frac{2}{3}x=4\\\\&\frac{1}{3}x=2\\\\&x=6\\\\\\&f(x)=\frac{1}{3}x+1&\textup{for }x< 2\\\\&-x+1=\frac{1}{3}x+1\\\\&-x=\frac{1}{3}x&\textup{for }x< 2\\\\&x=0\\\\\textup{L\o sning:}&x=\left\{\begin{matrix}0 \\6\end{matrix}\right. \end{array}$

Brugbart svar (0)

Svar #7
20. januar 2020 af AMelev

|x| betyder talværdien af x, hvor fortegnet er "smidt væk". Fx |3| = |-3| = 3
Hvis x ≥ 0, så er |x| = x, men hvis x ≤ 0, skal der skiftes fortegn, så |x| = -x, fx |-3| = -(-3) = 3

Beregning

$|x-2|-1=\frac{1}{3}x+1\Leftrightarrow |x-2|=\frac{1}{3}x+2\Leftrightarrow \left\{\begin{matrix} x-2=\frac{1}{3}x+2 & x-2\geq 0\Leftrightarrow x\geq 2\\ -(x-2)=\frac{1}{3}x+2 & x-2 < 0\Leftrightarrow x< 2\\ \end{matrix} \right. \Leftrightarrow \left\{\begin{matrix} x=\frac{1}{3}x+4 & x\geq 2\\ -x=\frac{1}{3}x & x< 2\\ \end{matrix} \right. \Leftrightarrow \left\{\begin{matrix} x=.... & x\geq 2\\ x=.... & x< 2\\ \end{matrix} \right. \Leftrightarrow x = .... \: \textup{eller }\: x = ....$

Grafisk

Vedhæftet fil:Udklip.JPG

Skriv et svar til: funktion og ligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.