Matematik

Løsning til differentialligning

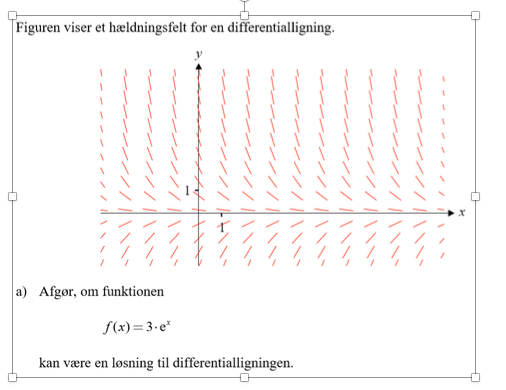
26. januar 2020 af Lei20 (Slettet) - Niveau: A-niveau

Kan det passe, at f(x) ikke er en løsning til differentialligningen?

Vedhæftet fil: Skærmbillede 2020-01-26 kl. 12.42.29.png

Brugbart svar (0)

Svar #1
26. januar 2020 af Mathias7878

$f'(x) = (3\cdot e^x)' = 3\cdot e^x$

Tangentens hældning i punket x = 1 giver f.eks.

$f'(1) = 3\cdot e^1 \approx 8.15$

hvilket fremgår tydeligt af figuren ikke er korrekt. Så nej funktionen er ikke en løsning til differentialligningen.

- - -

Brugbart svar (0)

Svar #2
26. januar 2020 af peter lind

Brugbart svar (0)

Svar #3
26. januar 2020 af peter lind

Svar #4
26. januar 2020 af Lei20 (Slettet)

#1
$f'(x) = (3\cdot e^x)' = 3\cdot e^x$

Tangentens hældning i punket x = 1 giver f.eks.

$f'(1) = 3\cdot e^1 \approx 8.15$

hvilket fremgår tydeligt af figuren ikke er korrekt. Så nej funktionen er ikke en løsning til differentialligningen.

Kan man formulere svaret til opgaven på denne måde?

a) Funktionen f(x) kan ikke være en løsning til differentialligningen. På grafen kan man se, at der er tale om eksponentiel aftagende vækst. Differentialligningen, der beskriver eksponentiel vækst, er på formen y´=k·y og den har løsningen y=C·e^kx hvilket er af samme form som løsningen f(x)=3·e^x, men da f(x) er voksende, kan det ikke være en løsning til differentialligningen.

Skriv et svar til: Løsning til differentialligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.