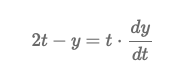Matematik

løsning til differentialligning

27. marts 2020 af Trojanskhest - Niveau: A-niveau

hejsa

er der nogen der kan forklare med ord hvordan i løser differentielligningen som er vedhæftet

Vedhæftet fil: Skærmbillede 2020-03-27 kl. 22.49.36.png

Brugbart svar (0)

Svar #1
27. marts 2020 af janhaa

integrating factor

Brugbart svar (0)

Svar #2
27. marts 2020 af Capion1

Skærmbillede 2020-03-27 kl. 22.49.36.png

Omskriv til $\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{2t-y}{t}=2-\frac{y}{t}$ og benyt panserformlen.

Svar #3
28. marts 2020 af Trojanskhest

okay er det så:

y'=2-y*1/t

som omskrives på formen h(x)=y'+y*g(x)

og løsningen bliver

y=e^-ln(t)*integralet af 2*e^ln(t) dx

eller er jeg helt ude og skide

Brugbart svar (0)

Svar #4
28. marts 2020 af Capion1

Det er helt rigtigt. Der skal så stå dt og ikke dx under integraltegnet.
Gør integrationen færdig.

Svar #5
28. marts 2020 af Trojanskhest

y=e^-ln(t)*integralet af 2*e^ln(t) dx

bliver så til

y=1/2*2t

som giver y=t.

Problemet er bare at min lærere siger at svaret er y=1/t+t

Brugbart svar (0)

Svar #6
28. marts 2020 af Capion1

Man får:

$y=e^{-\ln t}\int 2\cdot e^{\ln t}\textup{d}t=\frac{1}{t}\int 2t\textup{d}t$ $=\frac{1}{t}\left ( t^{2}+c \right )=t+\frac{c}{t}$ c er en vilkårlig konstant.

Svar #7
28. marts 2020 af Trojanskhest

kæft jeg er en kegle, TAAK for det. Det var ikke så svært alligevel

Brugbart svar (0)

Svar #8
28. marts 2020 af Capion1

Nej, - det var ikke svært. Panserformlen er god at ha' og er ikke svær at bruge. Man skal blot huske at få integrationskonstanten med til sidst.

Skriv et svar til: løsning til differentialligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.