Matematik

Opskriv en forskrift for denne harmoniske svingning

09. april 2020 af magnussh2 - Niveau: B-niveau

Jeg har fået stillet følgende opgave uden hjælpemidler:

Den vekselspænding vi benytter til mange el-apparater, kan beskrives som en harmonisk

svingning, der varierer som funktion af tiden med en amplitude pa° 310 volt og en frekvens pa° 50 Hz.

a) Opskriv en forskrift for denne harmoniske svingning

Hvilken ligning er nemmest at bruge til at opskrive den harmoniske svingning? Jeg tænker ikke at jeg kan bruge formen f(x) = A*sin(b*x + c) + k; da jeg med den vel mangler for mange variabler? Udfra teksten kan jeg jo kun komme frem til at a = 310 og f = 50

Håber der er nogen, som kan hjælpe mig med hvordan jeg kan løse opgaven. :))

Tak på forhånd!

Brugbart svar (1)

Svar #1
09. april 2020 af peter lind

Det kan du godt med c=0 og k=0

Svar #2
09. april 2020 af magnussh2

#1
Det kan du godt med c=0 og k=0

ahhh okay. Er det så frekvensen jeg skal bruge til at finde b? Hvordan kan jeg det?

Brugbart svar (0)

Svar #3
09. april 2020 af peter lind

b = 2π/T = 2πf hvor f er frekvensen

Brugbart svar (1)

Svar #4
10. april 2020 af ringstedLC

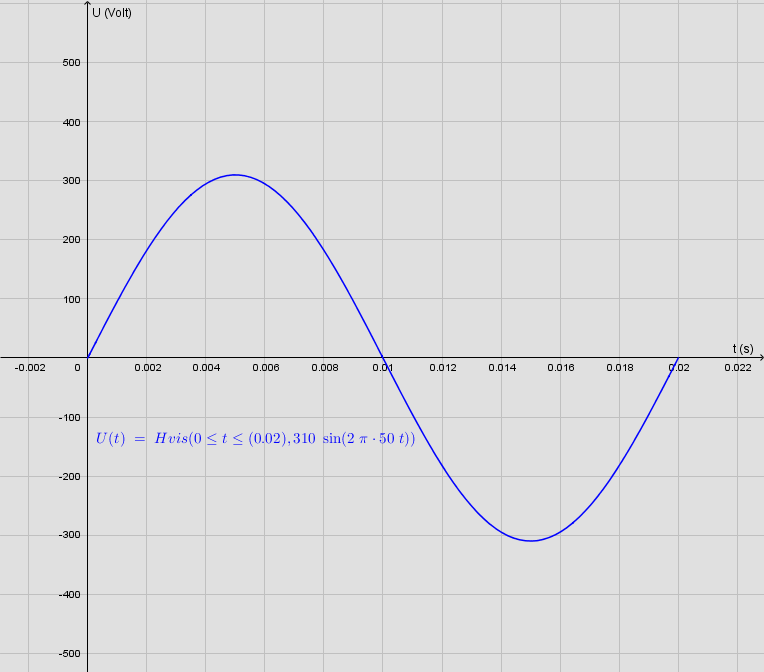
Da vekselspændingen "kan beskrives som en harmonisk svingning,", kan formen selvfølgelig anvendes:

$\begin{align*} U({\color{Red} t}) &= A\cdot \sin (\omega \cdot t-\varphi )+k \\ U(t) &= 310\cdot \sin (\omega \cdot t)\;,\;\varphi =0\;,\;k=0 \\ f &= \frac{1}{P}\Rightarrow P=\frac{1}{f}\Rightarrow \omega=\frac{2\pi}{P} =2\pi f \end{align*}$

Hvis du tegner den, anbefales det at sætte et interval:

$\begin{align*} U(t) &= 310\cdot \sin (2\pi f \cdot t)\;,\;0\leq t\leq \tfrac{1}{f}=0.02 \end{align*}$

og akse-forholdet skal sikkert justeres.

Svar #5
10. april 2020 af magnussh2

#4
Da vekselspændingen "kan beskrives som en harmonisk svingning,", kan formen selvfølgelig anvendes:

$\begin{align*} U({\color{Red} t}) &= A\cdot \sin (\omega \cdot t-\varphi )+k \\ U(t) &= 310\cdot \sin (\omega \cdot t)\;,\;\varphi =0\;,\;k=0 \\ f &= \frac{1}{P}\Rightarrow P=\frac{1}{f}\Rightarrow \omega=\frac{2\pi}{P} =2\pi f \end{align*}$

Hvis du tegner den, anbefales det at sætte et interval:

$\begin{align*} U(t) &= 310\cdot \sin (2\pi f \cdot t)\;,\;0\leq t\leq \tfrac{1}{f}=0.02 \end{align*}$

og akse-forholdet skal sikkert justeres.

nu spørger jeg måske dumt, men kan du forklare hvad der menes med P? Indtil videre er jeg med på hvordan jeg kommer hertil: f(x) = 310*sin(b*x);

Brugbart svar (1)

Svar #6
10. april 2020 af ringstedLC

#5: Fint, så har du jo forskriften. Jeg har bare brugt symbolerne som kendes i fysiken.

P er den som #3 benævner T:

$\begin{align*} P &= \text{periode}=\text{svingningstid} \\ f &= \text{frekvens} \end{align*}$

Svar #7
10. april 2020 af magnussh2

#6
#5: Fint, så har du jo forskriften. Jeg har bare brugt symbolerne som kendes i fysiken.

P er den som #3 benævner T:

$\begin{align*} P &= \text{periode}=\text{svingningstid} \\ f &= \text{frekvens} \end{align*}$

ahhh okay! Nu giver det mening. Tak til jer begge!

Brugbart svar (0)

Svar #8
10. april 2020 af ringstedLC

Vedhæftet fil:__0.png

Skriv et svar til: Opskriv en forskrift for denne harmoniske svingning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.