Hastighed og længste afstand fra punktet P

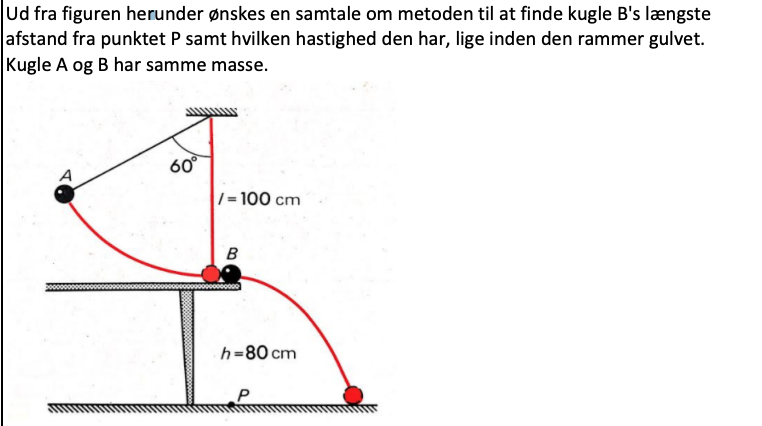
Givet: A bevæger sig i en cirkelbevægelse under påvirkning af tyndekraften og snorkraften.

Antagelse: A og B støder sammen i et fuldstændig elastisk sammenstød, hvor impuls og enegi er bevaret. Der ses bort fra gnidningskræfter (herunder luftmodstand) og snorens masse. Det antages endvidere, at B bevæger sig i en parabelbane.

#1. 

Man bruger P som nulpunkt for et koordinatsystem, hvor x-aksen går vandret mod højre og y-aksen går lodret opad.

I begge spørgsmål har man brug for at kende B's vandrette begyndelses-fart. Dette gøres ved at sætte ændring i potentiel energi for A lig med ændring i kinetisk energi for A. A's fart lige inden sammenstødet med B er lig med B's vandrette fart lige efter.

Ændring i potentiel energi for A er: ΔE_p = Δh·g·m, hvor Δh er forskel i højde for A fra start til bordhøjde, g er tyngde-accelerationen og m er massen af A. Formlen for ændring i kinetisk energi af A er: ΔE_k = 0,5·m·v², hvor v er A's fart lige før sammenstødet. Man har: 

ΔE_p = ΔE_k ⇒ Δh·g·m = 0,5·m·v² ⇒ v = √[2·Δh·g].
Her er Δh = 1,00m - 1,00m·cos(60°) = 1,00 m - (1,00 m ·0,5) = 0,5 m.
Dette giver: v = √[2·0,5 m·9,82 m·s^-2] ⇒ v = 3,13 m/s.

Man har følgende formler for B's afstand til P:
Vandret afstand: s_x(t) = (3,13 m/s)·t, dvs. proportional med med startfarten i x-aksens retning.
Lodret afstand: s_y(t) = -0,5·g·t² + 0,8 m, dvs. B starter i 0,8 m højde med den lodrette begyndelses-fart 0 og accelereres af tyngdekraften i negativ retning.

Svar 1)
Afstanden er s_x(t₁), hvor t₁ er det tidspunkt, hvor B rammer gulvet. Dette tidspunkt kan beregnes ud fra s_y(t), idet... 
s_y(t₁) = 0 ⇒ -0,5·g·t₁² + 0,80 m ⇒ 0,5·(9,82 m·s^-2)·t₁² = 0,80 m ⇒ t₁² = (0,80 m)/(0,5·(9,82 m·s^-2)) ⇒ 
t₁ = √[(0,80 m)/(0,5·(9,82 m·s^-2))] ⇒ t₁ = 0,404 s.
Dette indsættes: s_x(t₁) = (3,13 m/s)·(0,404 s) = 1,27 m

Svar 2)
B's fart lige inden den rammer gulvet kan beregnes ud fra B's kinetiske energi lige inden gulvet (ΔE_k(B)). Denne kan igen beregnes ved at lægge A og B's potentielle energier sammen (kan lade sig gøre, når de har samme masse): ΔE_p(A+B) = Δh·g·m. Her er Δh = 0,5 m + 0,8 m = 1,30 m. 
ΔE_k(B) = ΔE_p(A+B) ⇒ v = √[2·1,3 m·9,82 m·s^-2] ⇒ v = 5,05 m/s.

Hvis man skal beregne hastighedsvektoren, så er x-koordinaten 3,13 m/s og y-koordinaten: (-9,82 m·s^-2)·0,404 s = -3,97 m/s. Prøve: Hasighedsvektoren har følgende længde: √[3,13² + 3,97²] m/s ≈ 5,05 m/s, hvilket ses at passe med farten ovenfor.

#2...A's fart lige inden sammenstødet med B er lig med B's vandrette fart lige efter...

Dette følger af impulbevarelse i et fuldstændig elastisk sammenstød mellem to kugler med samme masse: m_A·v_A = m_B·v_B ⇒ v_A = v_B, da m_A = m_B.