Matematik

Sandsynlighed

26. maj 2020 af K22 - Niveau: A-niveau

Hvordan beregner jeg disse opgaver?

Jeg fik a) til 2/6 = 1/3

Vedhæftet fil: Skærmbillede 2020-05-26 kl. 21.05.12.png

Brugbart svar (0)

Svar #1
26. maj 2020 af Jones2929

9.a)

den har du regnet rigtigt.

9.b)

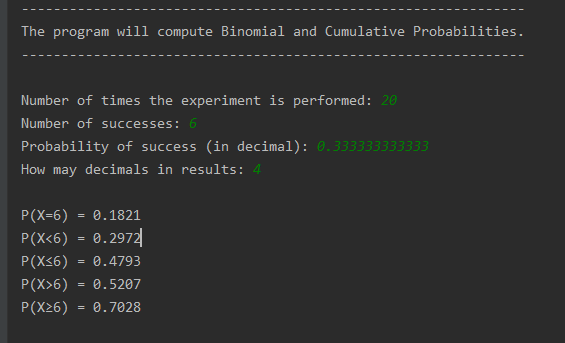
Du har regnet frem til, at antalsparameteren p = 0.33/33%. Du bruger formlen for sandsynlighedsfunktionen for binomialfordelt stokastisk variabel X: $P(X=r)=K(n,r)*p^r*(1-p)^{n-r}$ .

n er antalsparameteren, i vores tilfælde 20 (20 forsøg). Den lander på en blå side 6 ud af 20 gange. Dette er K(20,6).

Som jeg skrider frem kan jeg fornemme, at denne opgave er stillet med hjælpemidler. Ved udregning i Maple finder man, at sandsynligheden er 18%

9.c)

Man finder det igen i Maple. Sandsynligheden er 70%.

Brugbart svar (0)

Svar #2
26. maj 2020 af AMelev

a) OK!

X = antal blå, X ~ b(20,1/3)
b) P(X = 6) Benyt FS side 41 (252) eller CAS

c) P(X ≥ 6) Benyt CAS, evt via P(X ≥ 6) = 1 - P(X < 6) = 1 - P(X ≤ 5).

Svar #3
26. maj 2020 af K22

bliver b) ikke 18,4%? Du har skrevet 18%

Svar #4
26. maj 2020 af K22

Hvordan beregner jeg c)

Brugbart svar (0)

Svar #5
27. maj 2020 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Svar #6
27. maj 2020 af K22

Hvordan beregner man det vha. en formel?

Brugbart svar (0)

Svar #7
27. maj 2020 af PeterValberg

Se dette < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Svar #8
27. maj 2020 af K22

Men c) kan man ikke beregne vha. den formel, fordi den siger “mindst 6 gange”?

Brugbart svar (0)

Svar #9
27. maj 2020 af PeterValberg

Sandsynligheden for mindst 6 gange kan bestemmes som:

$P(X\geq 6) =1-P(X<6)= 1 - (P(X=0) + P(X=1) + .... + P(X=5))$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #10
27. maj 2020 af AMelev

Brug dit CAS-værktøj. Hvilket bruger du?

Brugbart svar (0)

Svar #11
27. maj 2020 af PeterValberg

#0 Hvis dit CAS-værktøj er TI-nspire, så har du flere muligheder:

Den sidste er nok den hurtigste :-)

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Svar #12
27. maj 2020 af K22

Jeg bruger wordmat. Kender ikke til Tl inspire eller maple

Brugbart svar (0)

Svar #13
27. maj 2020 af PeterValberg

Wordmat har en indbygget funktion, der kan udregne binomialfordelingen for dig

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Brugbart svar (0)

Svar #14
27. maj 2020 af PeterValberg

Alternativt kan du måske bruge KeHaTools, som er et plugin til MS Excel < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #15
27. maj 2020 af PeterValberg

Du skal dog være opmærksom på, at KeHaTools kan være lidt drilsk at installere i Excel...
Men den kan sagtens lave beregningerne :-)

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #16
27. maj 2020 af AMelev

Du kan også skrive direkte ind i Excel med BINOMIAL.FORDELING(j;n;p;SAND), som returnerer P(X ≤ j).
= 1-BINOMIAL.FORDELING(5;20;1/3;SAND) giver således 1 - P(X ≤ 5) = P(X ≥ 6).

Svar #17
27. maj 2020 af K22

Hvordan skrives det som er skrevet i 9#

Brugbart svar (0)

Svar #18
27. maj 2020 af AMelev

=1-BINOMIAL.FORDELING(0;20;1/3;FALSK)+ BINOMIAL.FORDELING(1;20;1/3;FALSK)+ BINOMIAL.FORDELING(2;20;1/3;FALSK)+ BINOMIAL.FORDELING(3;20;1/3;FALSK)+ BINOMIAL.FORDELING(4;20;1/3;FALSK)+ BINOMIAL.FORDELING(5;20;1/3;FALSK))

Svar #19
27. maj 2020 af K22

Men hvad med selve udregningen?

Brugbart svar (0)

Svar #20
27. maj 2020 af AMelev

Jeg misforstod dig måske - jeg troede, det var i Excel.

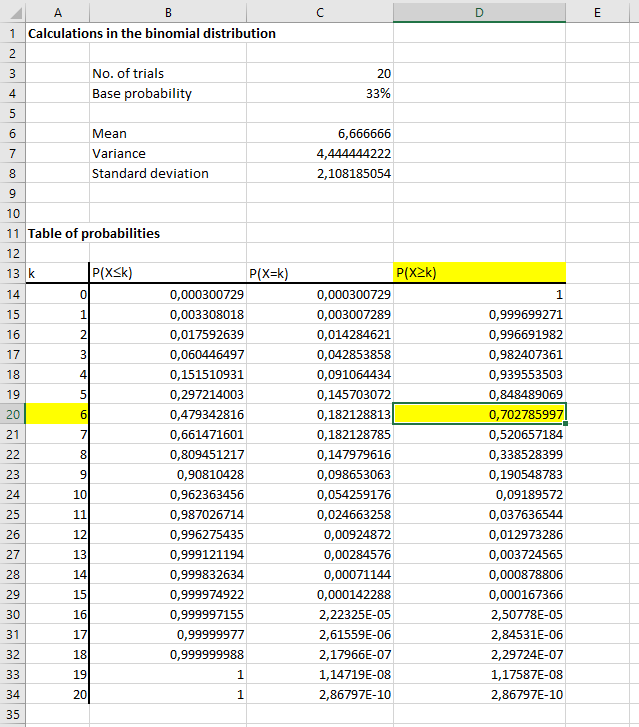
I Wordmat er det $1-(\frac{20!}{0!\cdot 20!}\cdot (\frac{1}{3})^0 \cdot (\frac{2}{3})^{20}+ (\frac{20!}{1!\cdot 19!}\cdot (\frac{1}{3})^1 \cdot (\frac{2}{3})^{19}+ (\frac{20!}{2!\cdot 18!}\cdot (\frac{1}{3})^2 \cdot (\frac{2}{3})^{18}+ (\frac{20!}{3!\cdot 17!}\cdot (\frac{1}{3})^3 \cdot (\frac{2}{3})^{17}+ (\frac{20!}{4!\cdot 16!}\cdot (\frac{1}{3})^4 \cdot (\frac{2}{3})^{16}+ (\frac{20!}{5!\cdot 15!}\cdot (\frac{1}{3})^5 \cdot (\frac{2}{3})^{15})$

men det er da en hulens masse skrivearbejde i forhold til bare at bruge Excel (jf. # 16) eller Excel via Wordmat, hvor du kan aflæse P(X ≤ 5) vha. skemaet efter at have ændret n og p, ved at lægge sandsynlighederne sammen for r = 0, 1, 2, 3, 4, 5.

Skriv et svar til: Sandsynlighed

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.