Matematik

linje og cirklen

30. juli 2020 af zainab48 - Niveau: B-niveau

Hej

Jeg har brug for hjælp, til den opgave, hvordan kan jeg tegne cirklen og linjen i samme koordinatsystem?

Vedhæftet fil: Billede1.png

Brugbart svar (0)

Svar #1
30. juli 2020 af StoreNord

Tegn cirklens rundkørslens centrum C og rundkørslens cirkel c med radius=1.
Tegn punktet startpunket A.
Lav en retningsvektor r.
Tegn et andet punkt B på linjen med kommandoen B=A+t*r.
Tegn linjen.
Nu kan du justere skyderen t, til B ligger på cirklen.

Brugbart svar (0)

Svar #2
30. juli 2020 af ringstedLC

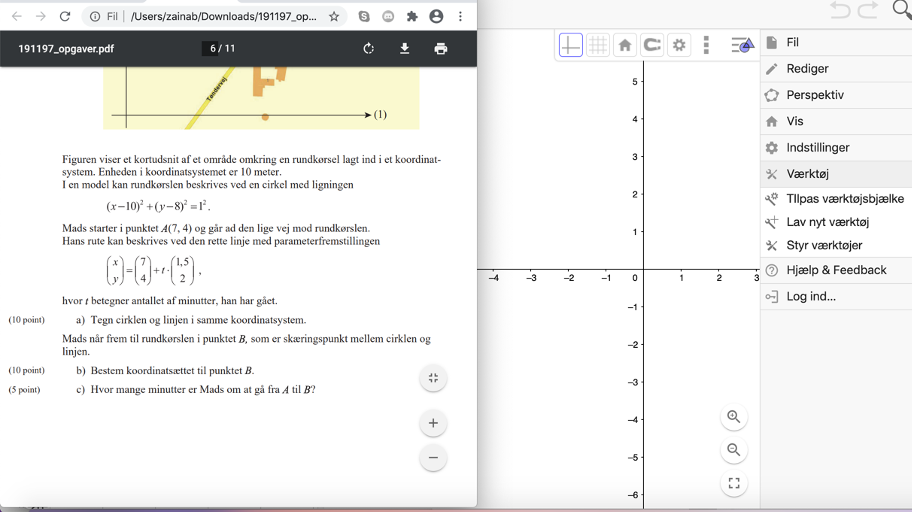
Vedhæft et billede af hele opgaven, og ikke af skærmen.

a) I GeoGebra:

$\begin{align*} \text{"Input:"}\;&(x-10)^2+(y-8)^2=1^2 \\ \text{"Input:"}\;&A:(7,4) \\ \text{"Input:"}\;&\text{linje}\Bigl(A,\text{vektor}\bigl((1.5,2)\bigr)\Bigr) \\ \end{align*}$

Svar #3
30. juli 2020 af zainab48

ser det rigtig ud?

Vedhæftet fil:Skærmbillede 2020-07-30 kl. 14.09.31.png

Brugbart svar (0)

Svar #4
30. juli 2020 af ringstedLC

#3: Ja.

b) Brug skæringsværktøjet til bestemme punkt B. Afgør udfra figuren hvilket af de to, der skal anvendes.

c) Indsæt B_xog løs ligningen:

$\begin{align*} B_x &= 7+t\cdot 1.5 \\ t &= \;? \end{align*}$

Svar #5
30. juli 2020 af zainab48

Mange tak for hjælp

Brugbart svar (0)

Svar #6
31. juli 2020 af mathon

$\small \small \small \begin{array}{lllllll} \textup{sk\ae ring:}\\& \begin{array}{lllllll} (7+1.5t-10)^2+(4+2t-8)^=1\\\\ (1.5t-3)^2+(2t-4)^2=1\\\\ 2.25t^2-9t+9+4t^2-16t+16=1\\\\ 6.25t^2-25t+24=0\\\\ x=\left\{\begin{array}{lll}\frac{25-\sqrt{25^2-4\cdot 6.25\cdot 24}}{2\cdot 6.25}=\frac{25-5}{12.5}=\frac{40}{25}=\frac{8}{5}=1.6\\\\ \frac{25+\sqrt{25^2-4\cdot 6.25\cdot 24}}{2\cdot 6.25}=\frac{25+5}{12.5}=\frac{60}{25}=\frac{12}{5}=2.4 \end{array}\right. \end{array}\\\\ \textup{sk\ae ringspunkter:}\\& \begin{array}{lllllll} S_1(7+1.5\cdot 1.6;4+2\cdot 1.6)=(9.4;7.2)\\\\ S_2(7+1.5\cdot 2.4;4+2\cdot 2.4)=(10.6;8.8) \end{array} \end{array}$

Brugbart svar (0)

Svar #7
03. august 2020 af mathon

$\small \small \small \small \small \begin{array}{lllllll} \textup{sk\ae ring:}\\& \begin{array}{lllllll} (7+1.5t-10)^2+(4+2t-8)^=1\\\\ (1.5t-3)^2+(2t-4)^2=1\\\\ 2.25t^2-9t+9+4t^2-16t+16=1\\\\ 6.25t^2-25t+24=0\\\\ t=\left\{\begin{array}{lll}\frac{25-\sqrt{25^2-4\cdot 6.25\cdot 24}}{2\cdot 6.25}=\frac{25-5}{12.5}=\frac{40}{25}=\frac{8}{5}=1.6\\\\ \frac{25+\sqrt{25^2-4\cdot 6.25\cdot 24}}{2\cdot 6.25}=\frac{25+5}{12.5}=\frac{60}{25}=\frac{12}{5}=2.4 \end{array}\right. \end{array}\\\\b)& \textup{sk\ae ringspunkter:}\\& \begin{array}{lllllll} S_1(7+1.5\cdot 1.6;4+2\cdot 1.6)=(9.4;7.2)\\\\ S_2(7+1.5\cdot 2.4;4+2\cdot 2.4)=(10.6;8.8) \end{array} \\\\ c)\\&\textup{gang-tid}=\left ( 2.4\;min- 1.6\;min\right )=0.8\;min=48\:s \end{array}$

Svar #8
03. august 2020 af zainab48

Mathon tak for hjælp

Skriv et svar til: linje og cirklen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.