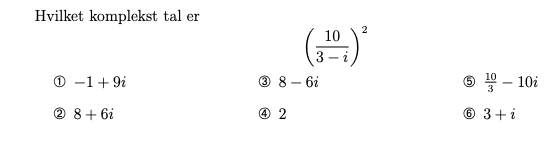Matematik

Modulus og argument

28. september 2020 af K22 - Niveau: Universitet/Videregående

Hvilke formler skal man bruge til at løse disse opgaver?

Vedhæftet fil: Skærmbillede 2020-09-28 kl. 11.23.27.png

Svar #1
28. september 2020 af K22

Anden opgave

Vedhæftet fil:Skærmbillede 2020-09-28 kl. 11.23.38.png

Brugbart svar (0)

Svar #2
28. september 2020 af mathon

Brugbart svar (0)

Svar #3
28. september 2020 af Capion1

z = OP
- 2z = -2OP
∀ z : modulus(z) ≥ 0

Brugbart svar (1)

Svar #4
28. september 2020 af mathon

$\small \begin{array}{lllll} -2=2\cdot e^{\textbf{\textit{i}}\cdot( -\pi)}\\\\ 2\cdot z=\left (2\cdot e^{\textbf{\textit{i}}\cdot( -\pi)} \right )\cdot \left ( 2\cdot e^ ^{\textbf{\textit{i}}\cdot( \frac{3\pi}{4})}\right )=2\cdot 2\cdot e^{\textbf{\textit{i}}\cdot \left ( \frac{-4\pi+3\pi}{4}\right )}=4\cdot e^{\textbf{\textit{i}}\cdot \frac{-\pi}{4}} \end{array}$

Brugbart svar (0)

Svar #5
28. september 2020 af Eksperimentalfysikeren

Multiplikation af to komplekse tal på modulus-argument-form udføres ved at multiplicere modulus for de to tal og addere argumenterne: (m₁,a₁)*(m₂,a₂) = (m₁*m₂,a₁+a₂)

Brugbart svar (0)

Svar #6
28. september 2020 af mathon

Svar #7
28. september 2020 af K22

Mathon hvordan går du fra -pi til -4pi/4

Brugbart svar (1)

Svar #8
28. september 2020 af mathon

$\small \begin{array}{lllll} -2\cdot \textbf{\textit{i}}=2\cdot e^{ \textbf{\textit{i}}\cdot (-\pi)}\cdot e^{\textbf{\textit{i}}\cdot \left ( \frac{\pi}{2} \right )}=2\cdot e^{\textbf{\textit{i}}\cdot \left ( \frac{-2\pi+\pi}{2} \right )}=2\cdot e^{\textbf{\textit{i}}\cdot\left ( \frac{-\pi}{2} \right )}\\\\ -2\textbf{\textit{i}}\cdot z=2\cdot e^{\textbf{\textit{i}}\cdot\left ( \frac{-\pi}{2} \right )}\cdot 2\cdot e^{\textbf{\textit{i}}\cdot \left ( \frac{3\pi}{4} \right )}=4\cdot e^{\textbf{\textit{i}}\cdot \frac{-2\pi+3\pi}{4}}=4\cdot e^{\textbf{\textit{i}}\cdot \frac{\pi}{4}} \end{array}$

Svar #9
28. september 2020 af K22

Jeg har forstået det. Mange tak. Kan du også hjælpe med denne her?

Vedhæftet fil:Skærmbillede 2020-09-28 kl. 12.05.37.png

Svar #10
28. september 2020 af K22

Og denne her

Vedhæftet fil:Skærmbillede 2020-09-28 kl. 12.07.11.png

Brugbart svar (0)

Svar #11
28. september 2020 af mathon

Brugbart svar (1)

Svar #12
28. september 2020 af mathon

$\small \begin{array}{lllll} z=3\cdot e^{\textbf{\textit{i}}\cdot \frac{\pi}{3}}\\\\ z^{-2}=\left ( 3\cdot e^{\textbf{\textit{i}}\cdot \frac{\pi}{3}} \right )^{-2}=3^{-2}\cdot\left ( e^{\textbf{\textit{i}}\cdot \frac{\pi}{3}} \right )^{-2}=\frac{1}{9}\cdot e^{\textbf{\textit{i}}\cdot \frac{\pi}{3}\cdot (-2)}=\frac{1}{9}\cdot e^{\textbf{\textit{i}}\cdot \frac{-2\pi}{3}} \end{array}$

Svar #13
28. september 2020 af K22

Hvad med det første billede jeg sendte?

Brugbart svar (0)

Svar #14
28. september 2020 af mathon

Brugbart svar (1)

Svar #15
28. september 2020 af mathon

$\small \small \begin{array}{lllll} \left ( \frac{10}{3-\textbf{\textit{i}} }\right )^2=\frac{10^2}{(3-\textbf{\textit{i}})^2}=\frac{100}{9-1-6\textbf{\textit{i}}}=\frac{100}{8-6\textbf{\textit{i}}}=\frac{100\left ( 8+ 6\textbf{\textit{i}}\right )}{\left (8-6\textbf{\textit{i}} \right )\cdot (8+6\textbf{\textit{i}})}=\frac{100\left ( 8+ 6\textbf{\textit{i}}\right )}{64+36}=\frac{100\left ( 8+ 6\textbf{\textit{i}}\right )}{100}=8+6\textbf{\textit{i}} \end{array}$

Brugbart svar (0)

Svar #16
28. september 2020 af AMelev

#0 & #1
Som alternativ til #8, kan du benytte Gangereglen i #5:
1) |-2| = 2 og arg(-2) = π, |z| = 2 og arg(z) = 3/4 π
$|-2\cdot z|=2\cdot 2=4$ og $arg(-2i\cdot z)=\pi+\frac{3}{4}\pi=(1+\frac{3}{4})\pi=\frac{7}{4}\pi$
NB! $\frac{7}{4}\pi=-\frac{\pi}{4}+2\pi$ , så det er i princippet ligegyldigt, om du bruger $\frac{7\pi}{4}$ eller $-\frac{\pi}{4}$ som argument, men hovedargumentet (det argument, der ligger i intervallet ]-π,π]) er ${\color{Red} -\frac{\pi}{4}}$ .

2) |-2i| = 2 og arg(-2i) = 3π/2, |z| = 2 og arg(z) = 3/4

$|-2i\cdot z|=2\cdot 2=4$
$arg(-2i\cdot z)=\frac{3}{2}\pi+\frac{3}{4}\pi=(\frac{3}{2}+\frac{3}{4})\pi=\frac{9}{4}\pi={\color{Red} \frac{1}{4}\pi}+2\pi$

De øvrige kan også bestemmes på denne måde.

Generelt følger af Gangereglen i #5, at |zⁿ| = |z|ⁿ og arg(zⁿ) = n·arg(z) (Potensreglen)
samt at |1/z| = 1/|z| og arg(1/z) = -arg(z) (Reciprokreglen).

Gangereglen og Reciprokreglen giver tilsammen Brøkreglen:
${\color{Red} |\frac{z}{w}|}=|z\cdot \frac{1}{w}|=|z|\cdot |\frac{1}{w}|=|z|\cdot \frac{1}{|w|}={\color{Red} \frac{|z|}{|w|}}$
${\color{Red} arg(\frac{z}{w})}=arg(z\cdot \frac{1}{w})=arg(z)+ arg(\frac{1}{w})= {\color{Red} arg(z)- arg(w)}$

3) z^-2 = 1/z²

4) Bestem først modulus og argument for 3- i
$|\frac{10}{3-i}|=\frac{10}{|3-i|}= ...$ og $arg(\frac{10}{3-i})=0-arg(3-i)= ...$ $arg(\frac{10}{3-i})=0-arg(3-i)= ...$

Svar #17
28. september 2020 af K22

Kan I hjælpe med denne her

Vedhæftet fil:Skærmbillede 2020-09-28 kl. 20.02.37.png

Brugbart svar (0)

Svar #18
28. september 2020 af AMelev

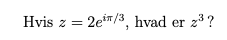
Ja, men det kan du også selv.
|z| = ? arg(z) = ?
Så bruger du potensreglen (jf #16) til at finde modulus og argument for z³, hvorefter du kan opskrive z³på polær form.

Svar #19
28. september 2020 af K22

Kan det passe, at r = 8

Svar #20
28. september 2020 af K22

Kan du vise, hvordan man gør det, så jeg er sikker på, at jeg gør det rigtigt?

Forrige 1 2 Næste

Der er 26 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.