Matematik
Ikke homogen lineær rekursion ligning
Hej Alle
jeg sidder med den opgave og den har drillet mig i lang tid,.Den handler om diskret matematik
er der nogle der kan hjælpe lidt. Opgave vedhæftes
Tak på forhånden.
Svar #2
18. oktober 2020 af Soeffi
#0.
a) Opskriv rekursionsligningen som: xn - 4·xn-1 + 3·xn-2 = 5·n + 6.
Gæt på en løsning på formen: x(n) = a·n2 + b·n + c. (x(n) = a·n + b dur ikke).
Følg i øvrigt: https://mjo.osborne.economics.utoronto.ca/index.php/tutorial/index/1/sod/t.
Svar #3
18. oktober 2020 af peter lind
Du må da have fået noget om løsningsmetoder for differeceligninger når du har fået sådan en opgave.
Du skal starte med at finde det karakteristiske polynomium og dernæst finde dets rødder
Se i det materiale du har fået eller se https://en.wikipedia.org/wiki/Recurrence_relation
Svar #4
18. oktober 2020 af DeepOcean
#2 jeg har gættet på x(n) = a·n + b men den virker ikke,,
Jeg har gætter på x(n) = a·n2 + b·n + c så får jeg meget komplex udtryk.!
Svar #5
18. oktober 2020 af Soeffi
#4. Jeg har gætter på x(n) = a·n2 + b·n + c så får jeg meget komplex udtryk.!
Jeg får dette:
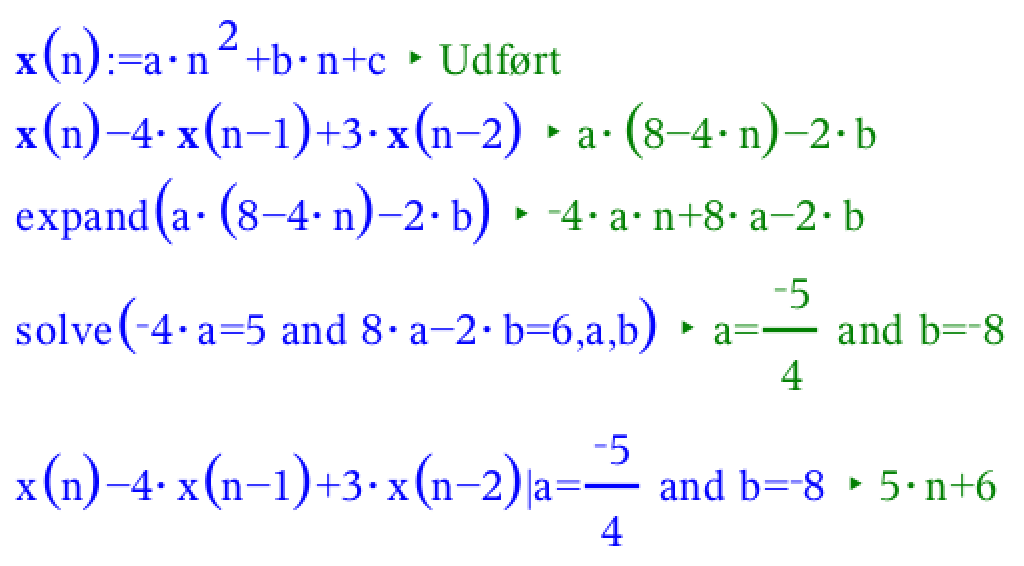
Svar #6
19. oktober 2020 af DeepOcean
#5 hvad mener du med Udført x(n) = a n2 +bn +c ..Du mener skal jeg finde rødderne nemlige n ?
skal jeg sætter den fundet a og b i ligning an2 +bn +c ?? .. hvad med c værdien ,,hvad skal jeg gøre ved den ?
Svar #7
19. oktober 2020 af peter lind
Du gætter jo bare i stedet for at læse hvordan man finder løsningen og løsningerne er ikke polynomier men eksponentalfunktioner.
Sæt yn = c*kn Hvis du sætter det ind i differensligningen kommer dufrem til at k er løsningen til et 2. grads polyninomium( kaldet det karakteristiske polynomium) løs så denne..
Du kan sammenligne med differentialligningen a*y'' + b*y' +c*y = f(x). Der faktisk megen ligheder mellem differentialligninger og differensligninger
Svar #8
19. oktober 2020 af Soeffi
#6. At løse rekursionsligningen: xn = 4·xn-1 - 3·xn-2 + 5·n + 6 betyder, at finde en funktion x(n), så x(n) - 4·x(n-1) + 3·x(n-2) = 5·n + 6. Her er samlet alle led, der indeholder x(n) på venstre side af lighedstegnet. Dette er den homogene del af rekursionsligningen. Den inhomogene del står på højre side.
Man gætter på en løsning af samme form som den inhomogene del dvs. et førstegradspolynomium: x(n) = a·n + b. Man får ved indsættelse: x(n)-4·x(n-1)+3·x(n-2) = a·n+b-4·(a·(n-1)+b)+3·(a·(n-2)+b). Man samler led, der indeholder n og led, der ikke gør: a·n+b-4·(a·(n-1)+b)+3·(a·(n-2)+b) = -2a. Det faktum, at der ikke er noget led, der indeholder n, betyder at et førstegradspolynomium ikke kan være en løsning.
Man prøver i stedet med et andengradspolynomium: x(n) = a·n2 + b·n + c. Man indsætter dette i den homogene ligning:
x(n) - 4·x(n-1) + 3·x(n-2) =
a·n2 + b·n + c - 4·(a·(n-1)2 + b·(n-1) + c) + 3·(a·(n-2)2 + b·(n-2) + c) =
-4a·n + (8a - 2b).
Dette er lig med 5n + 6, når a = -5/4, b = -8 og c ∈ R. Man vælger herefter c = 0, da man kun er bedt om een løsning.
Svar #9
19. oktober 2020 af peter lind
Det er da heller ikke en løsnig. Du kan bare se på det og sammenligne med hvad det skulle være. Du kan jo også ulejlige dig med at gøre prøve
Svar #10
19. oktober 2020 af Soeffi
#8. Dvs. en løsning til den inhomogene rekursionsligning er: x(n) = (-5/4)·n2 - 8·n
Prøve i sidste linje:
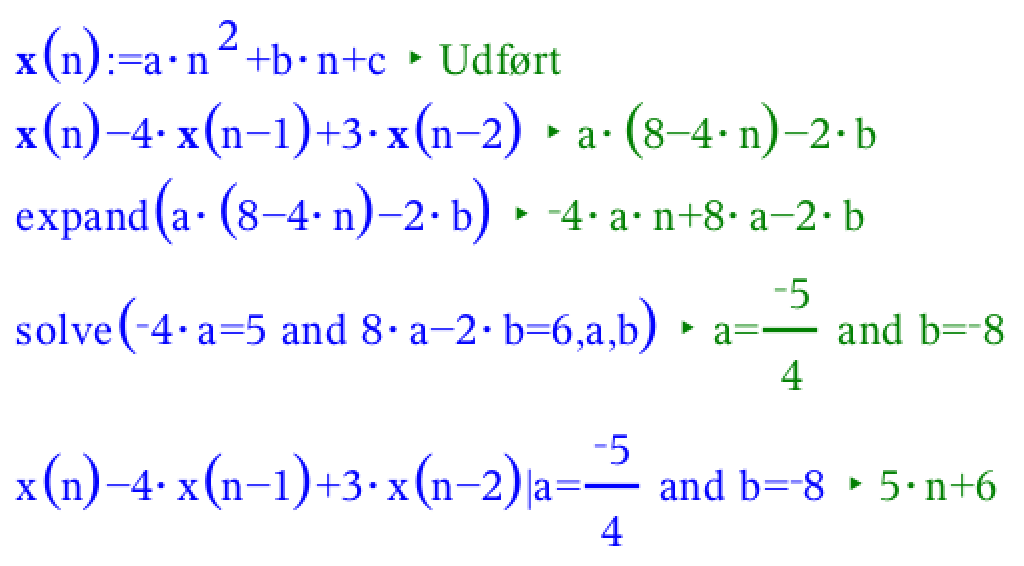
Svar #12
19. oktober 2020 af DeepOcean
# 8, 10
1000 Tak for Soeffi .Tak for at du har givet dig tid til en god forklaring .Nu forstår jeg bedre gæt metode og hvordan man indtaste i selv homogen ligning for at tjekke svar.
Svar #13
19. oktober 2020 af peter lind
Det er løsningen til den inhomogene ligning du finder. Løsningen til den homogene løsning kan i finde ved at indsætte x(n) = c*kn
Skriv et svar til: Ikke homogen lineær rekursion ligning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






