Matematik

løs ligning f(x)=g(x)

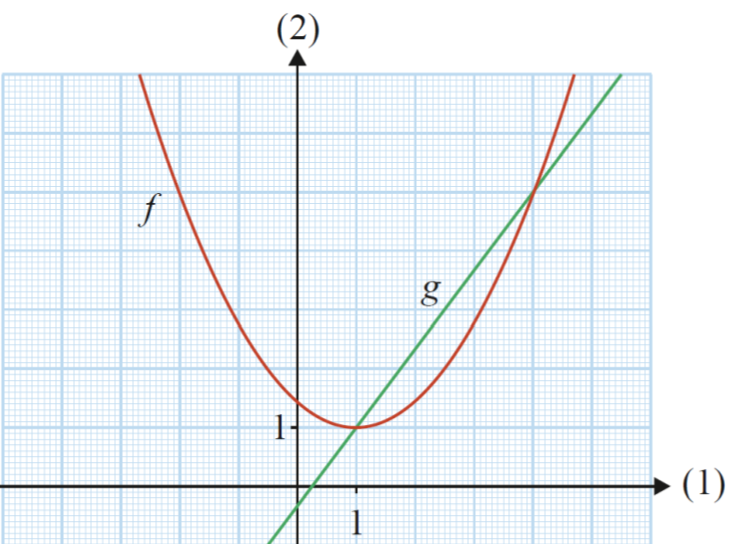
25. oktober 2020 af Jegis - Niveau: A-niveau

Benyt det vedlagte bilag til at løse ligningen f(x)=g(x)

Vedhæftet fil: f(x)=g(x)1.PNG

Brugbart svar (0)

Svar #1
25. oktober 2020 af Capion1

Aflæs de to x hvor de to kurver skærer hinanden.

Brugbart svar (0)

Svar #2
25. oktober 2020 af Anders521

#0 Aflæs skæringspunkterne ml. de grafer. 1.koordinaterne til punkterne vil være løsningerne til din ligning.

Svar #3
25. oktober 2020 af Jegis

Vil det så sige at løsningen er

f(1)=g(1) og f(4)=g(4)

Brugbart svar (0)

Svar #4
25. oktober 2020 af ringstedLC

#3: Nej. Men du er tæt på:

$\begin{align*} x_1 &= 1\;,\;x_2=4\Rightarrow f(x_1)=g(x_1)\wedge f(x_2)=g(x_2) \end{align*}$

Svar #5
25. oktober 2020 af Jegis

men var det ik det jeg skrev

Brugbart svar (0)

Svar #6
25. oktober 2020 af Capion1

Løsningen kan også skrives

$x=\left\{\begin{matrix} 1\\4 \end{matrix}\right.$

Brugbart svar (0)

Svar #7
25. oktober 2020 af Capion1

f (x) = ⁴/₉(x - 1)²+ 1
g (x) = ⁴/₃x - ¹/₃Løs da
⁴/₉(x - 1)² + 1 = ⁴/₃x - ¹/₃
Derfor hedder løsningen noget med x.

Svar #8
25. oktober 2020 af Jegis

Hvordan finder du frem til f(x) og g(x)

Brugbart svar (0)

Svar #9
25. oktober 2020 af Capion1

Du skal, i opgaven her, ikke finde hverken f eller g . Det har jeg kun gjort for at anskueliggøre, at når man
sætter f (x) = g (x) , får man en ligning i x , som løses.
I opgaven skal x-værdien/værdierne kun aflæses grafisk.

Svar #10
25. oktober 2020 af Jegis

super

Brugbart svar (0)

Svar #11
25. oktober 2020 af ringstedLC

#8

Hvordan finder du frem til f(x) og g(x)

Forskrifterne kan beregnes ved:

$\begin{align*} f(x) &= a\cdot \left ( x-x_{\,Top} \right )^2+y_{\,Top} \quad \left (\text{formel (74)} \right ) \\ f(x) &= a\cdot \left ( x-1 \right )^2+1 =ax^2-2ax+a+1 \\ f(4)=5 &= a\cdot (4-1)^2+1 \\ 4 &= 9a\Rightarrow a=\tfrac{4}{9} \\ f(x) &= \tfrac{4}{9}x^2-\tfrac{2\,\cdot \,4}{9}x+\tfrac{4}{9}+1 \\ f(x) &= \tfrac{4}{9}x^2-\tfrac{8}{9}x+\tfrac{13}{9} \\\\ g(x)=a\cdot x+b\;,\;a=\tfrac{y_2-y_1}{x_2-x_1}\;&,\;b=y_1-a\cdot x_1 \quad \left (\text{formel (78) og (79)} \right ) \\ a &= \tfrac{5-1}{4-1}=\tfrac{4}{3} \\ b &= 5-\tfrac{4}{3}\cdot 4=-\tfrac{1}{3} \\ g(x) &= \tfrac{4}{3}x-\tfrac{1}{3} \end{align*}$

Havde forskrifterne været kendt, kunne ligningen løses algebraisk:

$\begin{align*} f(x) &= g(x) \\ \tfrac{4}{9}x^2-\tfrac{8}{9}x+\tfrac{13}{9} &= \tfrac{4}{3}x-\tfrac{1}{3} \\ \tfrac{4}{9}x^2-\tfrac{8}{9}x-\tfrac{4}{3}x+\tfrac{13}{9}+\tfrac{1}{3} &= 0 \\ \tfrac{4}{9}x^2-\Bigl(\tfrac{8}{9}+\tfrac{4\,\cdot \,3}{3\,\cdot \,3}\Bigr)x +\Bigl(\tfrac{13}{9}+\tfrac{1\,\cdot \,3}{3\,\cdot \,3}\Bigr) &= 0 \\\tfrac{4}{9}x^2-\tfrac{20}{9}x+\tfrac{16}{9} &= 0 \\ 4x^2-20x+16 &= 0 \\ x &= \frac{-\left(-20\right)\pm\sqrt{\left(-20\right)^2-4\cdot 4\cdot 16}}{2\cdot 4} \quad \left (\text{formel (81)} \right ) \\ &= \frac{20\pm\sqrt{144}}{8} \\ &= \frac{20\pm 12}{8} \\ x=1&\vee x=4 \end{align*}$

Skriv et svar til: løs ligning f(x)=g(x)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.