Matematik

3 grads polymonie finde f(x), designe rutsjebane

01. april 2021 af 927 - Niveau: B-niveau

Hey:)

Jeg har en stor opgave for i matematik, og jeg sidder helt fast. Jeg skal designe en rutsjebane og en pool. Bunden af poolen og rutsjebanen selv, er en 3 grads polynomie. De eneste jeg får at vide det er toppunkterne. Som er givet med:

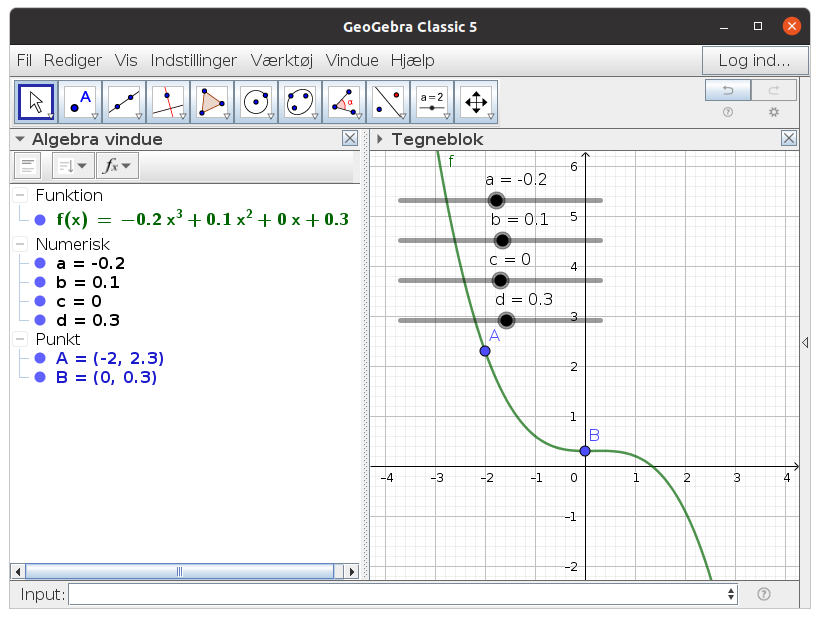
rutsjebane: (-2,2.3) og (0,0.3)

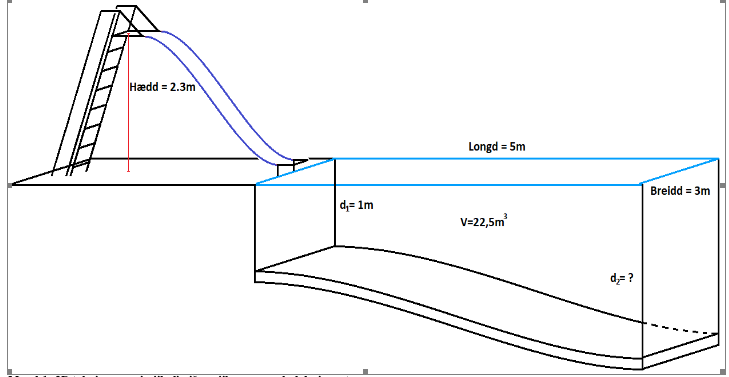
poolen: (0,-1) og (5,g(5))

jeg skal finde f(x) og g(x), men jeg ved ikke hvordan, nogle der kan hjælpe?

Brugbart svar (0)

Svar #1
01. april 2021 af AMelev

Læg lige et billede af hele opgaven op.

Brugbart svar (1)

Svar #2
01. april 2021 af StoreNord

Vedhæftet fil:Skærmbillede fra 2021-04-01 18-58-57.png

Svar #3
01. april 2021 af 927

her er rutsjebanen og poolen

Vedhæftet fil:Uden navn kopi..png

Svar #4
01. april 2021 af 927

og et til

Vedhæftet fil:167554730_1556126024582364_840335627856645283_n.jpg

Brugbart svar (0)

Svar #5
01. april 2021 af AMelev

#3 Det er jo kun figurskitsen, hvordan lyder opgaveformuleringen?

Svar #6
01. april 2021 af 927

opgaveformuleringen er: design rutsjebanen f(x) som en 3 grads polynomie, hvor hældningen i punktet (-2,2.3) er a=0 og hvor hældningen i punktet (0,0.3) er a=0

og i poolen er det det samme, men bare andre tal:)

Brugbart svar (0)

Svar #7
02. april 2021 af StoreNord

V=22,5 m³
Hvad skal du bruge den oplysning til?
Hvor bred er poolen?
Er den overhovedet rektangulær?

Svar #8
02. april 2021 af 927

her:)

Vedhæftet fil:Skærmbillede 2021-04-01 kl. 23.52.40.png

Brugbart svar (1)

Svar #9
02. april 2021 af StoreNord

Rutsjebanen:
f(x)=ax³+bx²+cx+d
Find f'
Opstil ligningen for f'(-2)=0
Opstil ligningen for f'(0)=0
Træk de to ligninger fra hinanden
Så har du at b= ?a ,hvor ? står for en koefficient

Brug så dette og f(0) og f(-2) til at finde at c=?a-1

Brug så b= ?a og c=?a-1 til at finde a af f(-2). (d kan du finde af f(0)=0,3)

Svar #10
02. april 2021 af 927

takk for hjælpen:)

Svar #11
02. april 2021 af 927

er poolen også bare det samme koncept eller?

Svar #12
02. april 2021 af 927

hvordan skal jeg trække ligningerne fra hinanden?, jeg fik f'(-2) = 8 og f'(0) = 0

Brugbart svar (1)

Svar #13
02. april 2021 af ringstedLC

#12: I (-2,2.3) er hældningen 0:

$\begin{align*} f'(-2) &= 0 \;{\color{Red} \neq} \;8 \end{align*}$

Differentier korrekt og opstil to ligninger med tre ubekendte (a, b og c), hvoraf c forsvinder ved subtraktion:

$\begin{array} {lllll} &\;\;\; \Bigl(a\cdot (-2)^2+b\cdot (-2)+c=0\;\; \Rightarrow \;\;-4a-2b+c=0\Bigr) \\ &-\Bigl(a\cdot \;\;\; (0)^2+b\cdot \;\;\;(0)+c=0\;\; \Rightarrow \qquad\qquad\quad\;\;\,c=0\Bigr) \\ &\text{------------------------------------------------------------------------} \\ &= \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\; -4a-2b=0 \end{align*}$

Brugbart svar (1)

Svar #14
02. april 2021 af ringstedLC

Brugbart svar (1)

Svar #15
02. april 2021 af ringstedLC

#11:

Pool: Udfra den generelle forskrift opstilles en reduceret forskrift og dens afledede:

$\begin{align*} g(x) &= ax^3+bx^2+cx+d \\ g(0)=-1\wedge g'(0)=0 &\Rightarrow \left \{ c,d \right \}=\left \{ ?,? \right \} \\ &\Rightarrow \left\{\begin{matrix} g(x)=...\\ g'(x)=...\end{matrix}\right. \end{align*}$

Volumet bruges først til bestemmelse af den absolutte værdi af det bestemte integrale og dernæst til:

$\begin{align*} V=22.5 &= \text{bredde}\cdot \left |\int_{0}^{5}\!g(x)\,\mathrm{d}x \right | \\ \left |\int_{0}^{5}\!g(x)\,\mathrm{d}x \right | &= \frac{22.5}{\text{bredde}} \\ g(x)<0\;,\;0\leq x\leq5\Rightarrow \int_{0}^{5}\!g(x)\,\mathrm{d}x &= -\left (\frac{22.5}{\text{bredde}}\right ) \end{align*}$

Løs ligningssystemet:

$\begin{align*} \int_{0}^{5}\!g(x)\,\mathrm{d}x &= -\left (\frac{22.5}{\text{bredde}}\right ) \wedge g'(5)=0\Rightarrow \left \{ a,b \right \}=\left \{ ?,? \right \} \end{align*}$

Brugbart svar (0)

Svar #16
02. april 2021 af StoreNord

#12
Svaret på dit spørgsmål er: Nej. Det er forkert.

Det er chokerende, at du ikke kender "Lige store koefficienters metode". Koefficienten til c er ens i de 2 ligninger, som RingstedLC trækker fra hinanden. Derfor bliver differencen 0 og så kan han beregne, b udtrykt ved a.

Svar #17
02. april 2021 af 927

yeah:D men jeg har aldrig lært det, mit skolesystem er lidt anderledes

Brugbart svar (0)

Svar #18
02. april 2021 af AMelev

Det er legalt i denne opgave at bruge CAS, så brug bare det til at løse flere ligninger med flere ubekendte - her tre.

Jeg tror faktisk ikke, at lige store koefficienters metode er standard, selv om det er det smarteste i mange tilfælde. I folkeskolen er substitutionsmetoden den gængse, og hvis metoden så ikke er taget op i gymnasiet, er den ukendt.

Brugbart svar (0)

Svar #19
03. april 2021 af StoreNord

Det kan godt være, at #0's lærer har en speciel mening om, hvilket metoder og værktøjer der skal bruges.
Det må vi hellere få noget at vide om.
???

Svar #20
03. april 2021 af 927

min lærer er meget bestemt om hvordan man skal sætte det op, men i dette tilfælde tror jeg at det er en smule lige meget

Forrige 1 2 3 Næste

Der er 57 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.