Matematik

06. april 2021 af maria2016 - Niveau: C-niveau

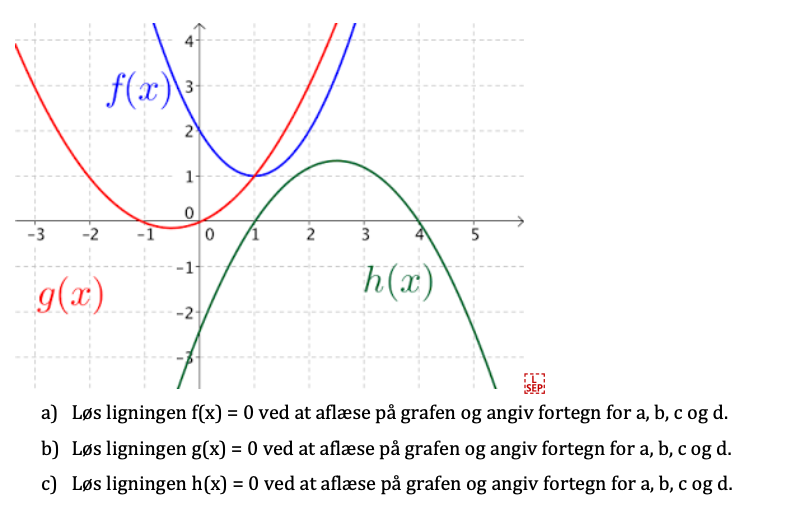
Hej jeg håber nogle kan hjælpe med denne opgave. Jeg er lidt i tvivl om hvordan jeg grafisk skal løse ligningen f(x) = 0, derudover vil jeg lige være sikker på om at det er rigtig at når man skal angive fortegn for a, b, c og d, ser således ud at grafen f(x) er a positiv, b er positiv, c er positiv og d har ingen løsninger. H(x) er a negativ, b negativ, c. negativ og d har to løsninger. G(x) er a positiv, b positiv,, c positiv og d har to løsninger.

På forhånd tak

Vedhæftet fil: Skærmbillede 2021-04-06 kl. 14.28.33.png

Brugbart svar (0)

Svar #1
06. april 2021 af mathon

Brugbart svar (0)

Svar #2
06. april 2021 af mathon

d er en talværdi og har ikke løsninger.

Brugbart svar (0)

Svar #3
06. april 2021 af mathon

$\small \begin{array}{llllllll} \textbf{a)}\\& f(x)=0&x\in \varnothing &a>0&b<0&c>0&d<0\\\\\textbf{b)}\\& g(x)=0&x\in \left \{ -1,0 \right \} &a>0&b>0&c=0&d>0\\\\\textbf{c)}\\& h(x)=0&x\in \left \{ 1,4 \right \} &a<0&b>0&c<0&d>0 \end{array}$

Brugbart svar (0)

Svar #4
06. april 2021 af AMelev

#0
Jeg er lidt i tvivl om hvordan jeg grafisk skal løse ligningen f(x) = 0.

Grafen for f skærer ikke 1.aksen, ligningen f(x) = 0 har ingen løsninger.

..., derudover vil jeg lige være sikker på om at det er rigtig at når man skal angive fortegn for a, b, c og d, ser således ud at vedrørende grafen f(x) er
a positiv, da parablen har grenene opad,
Toppunktets 1.koordinat $x_T=\frac{-b}{2a}\Leftrightarrow b=-2a\cdot x_T$
b er positiv, negativ, da både x_T og a er positive
c er positiv, da c er værdien i x =0 og
d er negativ, da f(x) = 0 ikke har løsninger. har ingen løsninger.

Hh(x):
a negativ, da ....
b negativ, da ....
c. negativ, da .... og
d positiv, da h(x) = 0 har to løsninger.

G(x)
a positiv, da ....
b positiv, da ....
c positiv nul, da .... og
d har to løsninger.

Svar #5
06. april 2021 af maria2016

Mange tak for hjælpen

Skriv et svar til: Matematik

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.