Matematik

Trigonometri

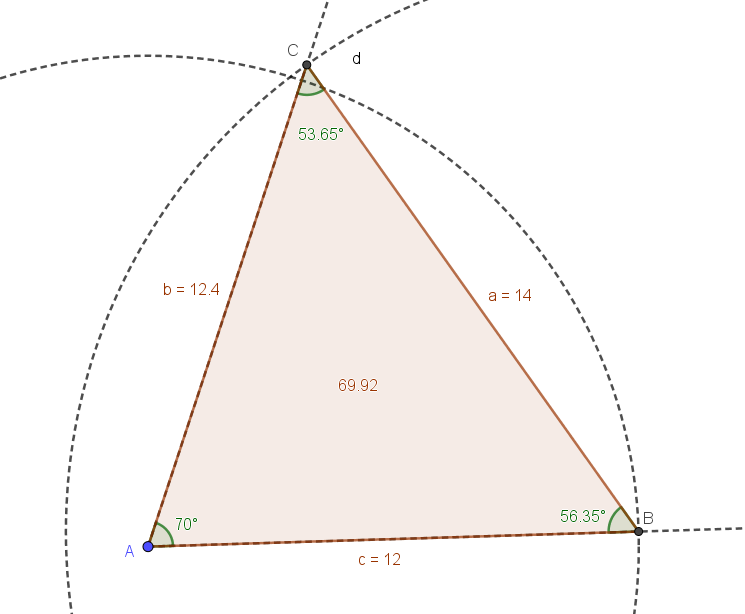
03. maj 2021 af jasmin1234561 - Niveau: C-niveau

En trekant har følgende oplysninger: A = 70 grader, a = 14, c = 12.

a) beregn vinkel C.

b) beregn vinkel B samt b

c) beregn arealet af trekanten

Brugbart svar (0)

Svar #1
03. maj 2021 af PeterValberg

a) Benyt en sinusrelation

b) Benyt at A + B + C = 180º
Benyt en sinus- eller cosinusrelation til bestemmelse af b

c) Benyt "Den halve appelsin"

$T_{ABC}=\tfrac12\cdot a\cdot b\cdot\sin(C)$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
03. maj 2021 af mathon

$\begin{array}{llll} \textbf{a)}\\&& c<a\Leftrightarrow 0<C<70\degree\\\\&& \frac{\sin(C)}{12}=\frac{\sin(70\degree)}{14}\\\\&& C=\sin^{-1}\left (\frac{12\cdot \sin(70\degree)}{14} \right ) \end{array}$

Brugbart svar (0)

Svar #3
03. maj 2021 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #4
03. maj 2021 af PeterValberg

Der finders en fantastisk hjemmeside,
du kan bruge til at kontrollere dine resultater:

< cossincalc.com >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #5
04. maj 2021 af mathon

$\begin{array}{llllll}\textbf{b)}\\&& b=a\cdot \cos(C)+c\cdot \cos(70\degree)=14\cdot \cos(53.6538)+12\cdot \cos(70\degree)=12.4015\\\\&& B=\cos^{-1}\left ( \frac{a^2+c^2-b^2}{2\cdot a\cdot c} \right )=\cos^{-1}\left ( \frac{14^2+12^2-12.4015^2}{2\cdot 14\cdot 12} \right )=56.35\degree\\\\& \textup{vinkelsum:}&\left (70+56.35+53.65 \right )\degree=180\degree \end{array}$

Skriv et svar til: Trigonometri

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.