Fysik

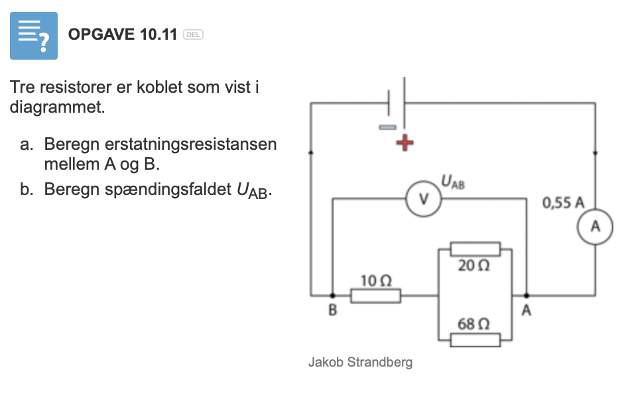
Spændingsfald og erstatningsresistansen

21. juli 2021 af saraelsayed - Niveau: B-niveau

Hej, jeg har lige lidt problemer med en opgaver. Jeg fik den første til 25 ohm og den anden til 45 V men er ikke sikker på at det er rigtigt

Vedhæftet fil: studienett.png

Brugbart svar (0)

Svar #1
21. juli 2021 af ringstedLC

Brugbart svar (0)

Svar #2
21. juli 2021 af ringstedLC

a. Det lyder rimeligt.

Dog; når strømmen er opgivet med to decimaler, bør du også regne med to decimaler:

$\begin{align*} \frac{1}{R_e} &= \frac{1}{R_1}+\frac{1}{R_2} \Rightarrow R_e=\frac{R_1R_2}{R_1+R_2} \\ R_{AB} &= R_3+R_e \\ &= 10\,\Omega+\left (\frac{20\cdot 68}{20+68} \right )\Omega=25.45\,\Omega \end{align*}$

b. Det er ikke rigtigt:

$\begin{align*} U_{AB} &= R_{AB}\cdot I \end{align*}$

Svar #3
21. juli 2021 af saraelsayed

Hej ringstedLC, jeg har prøvet at regne det ud og fik det her. Kan det være rigtigt?

Vedhæftet fil:Skærmbillede 2021-07-21 kl. 18.13.52.png

Brugbart svar (0)

Svar #4
21. juli 2021 af Eksperimentalfysikeren

Du har skrevet forkert. De 25 Ohm bliver pludselig til 35 Ohm

#2 Det er ikke antallet af decimaler, der skal bevares, men antallet af betydende cifre. Derfor er det korrekt at angive resultatet som 25 Ohm.

Brugbart svar (0)

Svar #5
21. juli 2021 af ringstedLC

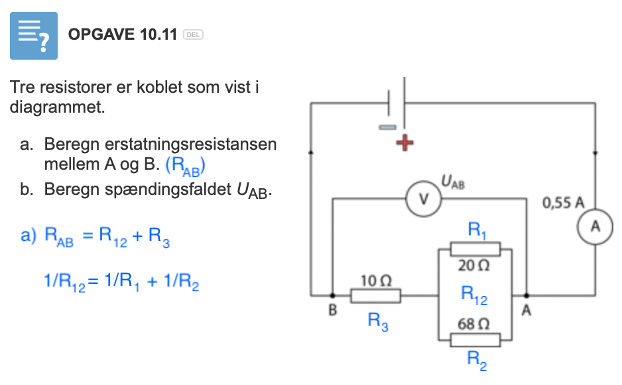
#3: Nej, fordi du roder; modstanden på 10 Ω er bl. a. med to gange i beregningen af den samlede modstand R_AB.

Erstatningsmodstanden for parallelkoblingen:

$\begin{align*} \frac{1}{R_\textup{e}} &= \frac{1}{R_1}+\frac{1}{R_2} \\ \frac{1}{R_\textup{e}}\cdot R_\textup{e} &= \left (\frac{1}{R_1}+\frac{1}{R_2} \right )\cdot R_\textup{e} \\ \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}} &= R_\textup{e} \\ \left (\frac{1}{R_1}+\frac{1}{R_2} \right )^{\!-1}\! &= R_\textup{e}\;{\color{Red} \neq }\;\frac{1}{R_\textup{e}}\;,\;R_\textup{e}\neq 1 \\ \end{align*}$

I resten er metoden OK.

Brugbart svar (0)

Svar #6
21. juli 2021 af Soeffi

#0. Brug evt. nedenstående notation:

Vedhæftet fil:2018479.png

Brugbart svar (0)

Svar #7
21. juli 2021 af ringstedLC

Alternativ for erstatningsmodstanden:

$\begin{align*} \frac{1}{R_\textup{e}} &= \frac{1}{R_1}+\frac{1}{R_2} \\ &= \frac{1\cdot R_2}{R_1\cdot R_2}+\frac{R_1\cdot 1}{R_1\cdot R_2} \\ \frac{1}{R_\textup{e}} &= \frac{R_1+R_2}{R_1\cdot R_2} \\ R_{e}\cdot \left (R_1+R_2\right ) &= R_1\cdot R_2 \\ R_{e} &= \frac{R_1\cdot R_2}{R_1+R_2}\quad \textup{ (brugt i \#2)} \end{align*}$

Ved tre el. flere modstande kan erst.-modst. beregnes ved at beregne dem parvist.

Svar #8
22. juli 2021 af saraelsayed

Okay, tak for alle jeres svar, men nu roder jeg mellem dem. Her er svaret for a, men hvilken formel skal jeg så bruge til b?

Vedhæftet fil:Skærmbillede 2021-07-22 kl. 09.34.42.png

Brugbart svar (0)

Svar #9
22. juli 2021 af mathon

$\small \begin{array}{lllllll} \textbf{b.}\\& R_{AB}=\left ( 10\;\Omega \right )+\left (\frac{\left ( 20\;\Omega \right )\cdot\left ( 68\;\Omega \right ) }{\left ( 20\;\Omega \right )+\left ( 68\;\Omega \right )} \right )=25.4545\;\Omega\\\\& U_{AB}=R_{AB}\cdot I=(25.4545\;\Omega)\cdot \left ( 0.55\;A \right ) \end{array}$

Brugbart svar (0)

Svar #10
22. juli 2021 af Eksperimentalfysikeren

#8 Din udregning er korrekt, men når resultatet skal angives, er det 25Ω, ikke 25,45Ω.

Tallene, der indgår i udregningen har 2 betydende cifre, Derfor skal resultatet også angives med 2 betydende cifre. Mellemresultater bør have 1 til 2 flere betydende cifre for at undgå afrundingsfejl.

Skriv et svar til: Spændingsfald og erstatningsresistansen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.