Matematik

Bestem fodlængden af højden fra A på BC

19. januar 2022 af helpn - Niveau: A-niveau

Hej. Er der en der kan hjælpe med spørgsmål b og c her??

Brugbart svar (0)

Svar #1
19. januar 2022 af mathon

$\small \begin{array}{llllll} \textbf{a.}\\&& \overrightarrow{AB}=\begin{pmatrix} 5\\3 \end{pmatrix}\\\\&& \overrightarrow{BC}=\begin{pmatrix} 8\\-2 \end{pmatrix}\\\\&& \overrightarrow{AB}_{\overrightarrow{BC}}=\frac{\overrightarrow{AB}\cdot \overrightarrow{BC}}{\overrightarrow{BC}^2}\cdot \overrightarrow{BC}=\frac{\bigl(\begin{smallmatrix} 5\\3 \end{smallmatrix}\bigr)\cdot \bigl(\begin{smallmatrix} 8\\-2 \end{smallmatrix}\bigr)}{8^2+(-2)^2}\cdot \begin{pmatrix} 8\\-2 \end{pmatrix}= \end{array}$

Svar #2
19. januar 2022 af helpn

Mangler hjælp til spørgsmål b og spørgsmål c :)

Brugbart svar (0)

Svar #3
19. januar 2022 af mathon

$\small \begin{array}{llllll} \textbf{b.}\\& \overrightarrow{OF}=\overrightarrow{OB}+ \overrightarrow{AB}_{\overrightarrow{BC}} \\\\&& \end{array}$

Brugbart svar (0)

Svar #4
19. januar 2022 af mathon

Hvis du ikke tegner det, kan du næppe regne det.

Brugbart svar (0)

Svar #5
19. januar 2022 af mathon

$\small \begin{array}{llllll} \textbf{c.}\\&\textbf{Pythagoras:}\\&& \left | AF \right |^2+\left |\frac{\overrightarrow{AB}\cdot \overrightarrow{BC}}{\left | \overrightarrow{BC} \right |} \right |^2=\left | \overrightarrow{AB} \right |^2 \end{array}$

Svar #6
19. januar 2022 af helpn

Forstår ikke helt dit svar til b. desværre... Hvad er vector OB?

Svar #7
19. januar 2022 af helpn

Er egentlig også stadig i tvivl om løsningen til spørgsmål c...

Brugbart svar (0)

Svar #8
19. januar 2022 af ringstedLC

$\begin{align*} \overrightarrow{OB} &= \binom{x_B-0}{y_B-0}\quad\textup{er stedvektoren for }B \end{align*}$

Brugbart svar (0)

Svar #9
20. januar 2022 af mathon

$\small \small \begin{array}{llllll} \textbf{c.}\\&\textbf{Pythagoras:}\\&& \left | AF \right |^2+\left |\frac{\overrightarrow{AB}\cdot \overrightarrow{BC}}{\left | \overrightarrow{BC} \right |} \right |^2=\left | \overrightarrow{AB} \right |^2\\\\&& \left | AF \right |^2+\left ( \sqrt{17} \right )^2=\left ( \sqrt{34} \right )^2\\\\&& \left | AF \right |^2=34-17=17\\\\&& \left | AF \right |=h_a=17 \end{array}$

Brugbart svar (0)

Svar #10
20. januar 2022 af mathon

$\small \small \begin{array}{llllll} \textbf{b.}\\& \overrightarrow{OF}=&\overrightarrow{OB}+ \overrightarrow{AB}_{\overrightarrow{BC}} \\\\&&\begin{pmatrix} 6\\5 \end{pmatrix} +\begin{pmatrix} 8\sqrt{17}\\ -2\sqrt{17} \end{pmatrix}=\begin{pmatrix} 6+8\sqrt{17}\\ 5-2\sqrt{17} \end{pmatrix}\\\\&F=&\left (6+8\sqrt{17}, -2\sqrt{17} \right )\quad \textup{da et punkt og dets stedvektor har \textbf{samme} koordinater} \end{array}$

Brugbart svar (0)

Svar #11
20. januar 2022 af mathon

korrektion:

$\small \small \small \small \begin{array}{llllll} \textbf{c.}\\&\textbf{Pythagoras:}\\&& \left | AF \right |^2+\left |\frac{\overrightarrow{AB}\cdot \overrightarrow{BC}}{\left | \overrightarrow{BC} \right |} \right |^2=\left | \overrightarrow{AB} \right |^2\\\\&& \left | AF \right |^2+\left ( \sqrt{17} \right )^2=\left ( \sqrt{34} \right )^2\\\\&& \left | AF \right |^2=34-17=17\\\\&& \left | AF \right |=h_a={\color{Red} \sqrt{17}} \end{array}$

Brugbart svar (0)

Svar #12
20. januar 2022 af Soeffi

#0. Løsning i Geogebra, fodpunkt kaldet D.

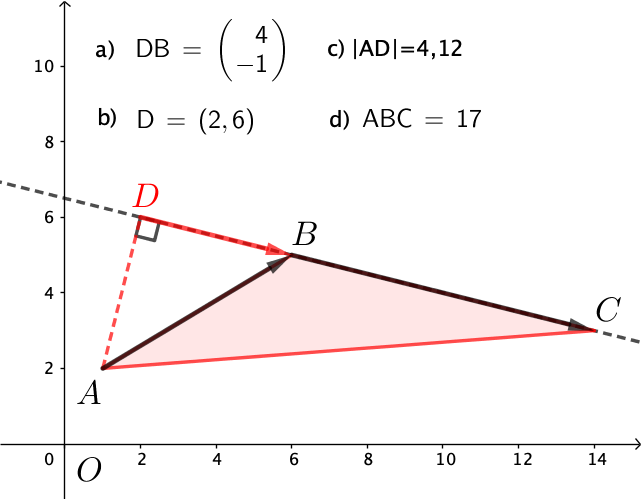
Vedhæftet fil:Untitled.png

Svar #13
20. januar 2022 af helpn

#10

Du får projektionen af vector AB på vector BC til $\left(\begin{array}{c} 8 \sqrt{17} \\ -2 \sqrt{17} \end{array}\right)$ . Nu har jeg regnet det både manuelt og med CAS, og får i begge tilfælde, at svaret er $\left(\begin{array}{c} 4 \\ -1 \end{array}\right)$ ?

Svar #14
20. januar 2022 af helpn

Desuden er svarene til spørgsmål b ikke de samme i hhv. #10 og #12, så er endnu mere forvirret over hvad den korrekte løsning er nu...

Brugbart svar (1)

Svar #15
21. januar 2022 af mathon

Jeg har en tegn- og regnefejl i vektorudtrykket.
I det følgende skiftes F $\small \rightarrow$ D:

$\small \small \small \begin{array}{llllll} \textbf{b.}\\& \overrightarrow{OD}=&\overrightarrow{OB}+ \overrightarrow{BD}=\overrightarrow{OB}-\overrightarrow{AB}_{\overrightarrow{BC}}= \\\\&&\begin{pmatrix} 6\\5 \end{pmatrix} -\begin{pmatrix} 4\\ -1 \end{pmatrix}=\begin{pmatrix} 2\\ 6 \end{pmatrix}\\\\&D=&\left (2, 6 \right )\quad \textup{da et punkt og dets stedvektor har \textbf{samme} koordinater} \end{array}$

Skriv et svar til: Bestem fodlængden af højden fra A på BC

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.