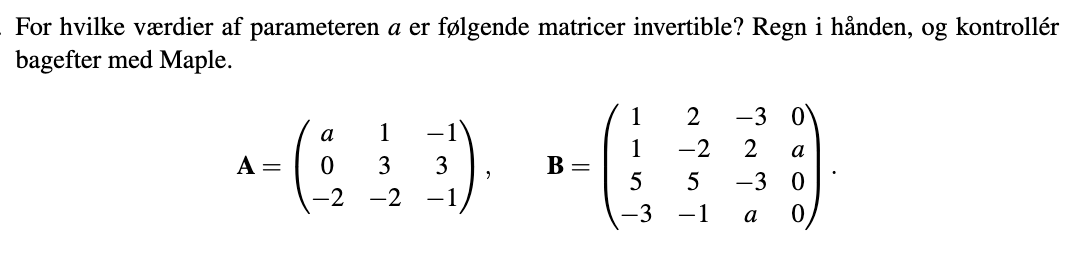Matematik

Hjælp til opgave der omhandler invertible matricer.

27. februar 2022 af vilana - Niveau: Universitet/Videregående

Hej. Jeg kan ikke helt se hvordan jeg skal løse denne opgave. Hvordan finder jeg værdierne for a?

Vedhæftet fil: Skærmbillede 2022-02-27 kl. 12.42.36.png

Brugbart svar (0)

Svar #1
27. februar 2022 af Al81

Kender du en metode der kan afgøre om en matrice er invertibel?

Svar #2
27. februar 2022 af vilana

Ved udføre reduced echelon på matricen? eller tjekke determinant. men forstår ikke det med man bestemmer for a

Brugbart svar (0)

Svar #3
27. februar 2022 af Soeffi

#0. Indsætter billede.

Brugbart svar (1)

Svar #4
27. februar 2022 af Soeffi

#0. En matrix er invertibel, hvis og kun hvis dens determinant er forskellig fra 0. Benyt desuden at determinanten til en matrix ikke ændres ved række- og søjleoperationer, samt at determinanten til en trekantsmatrix er produktet af diagonalelementerne. For A får man:

$\\ \begin{pmatrix} a & 1 & -1\\ 0 & 3 & 3 \\ -2 & -2 & -1 \end{pmatrix}\overrightarrow{_{S_3-S_1}} \begin{pmatrix} a & 2 & -2\\ 0 & 3 & 0 \\ -2 & -2 & 1 \end{pmatrix}\overrightarrow{_{R_1+2R_3}} \begin{pmatrix} a-4 & -2 & 0\\ 0 & 3 & 0 \\ -2 & -2 & 1 \end{pmatrix}\overrightarrow{_{R_1+2/3R_2}} \\\\\\ \begin{pmatrix} a-4 & 0 & 0\\ 0 & 3 & 0 \\ -2 & -2 & 1 \end{pmatrix}$

Dette viser, at A har determinanten (a-4)·3. Dvs. at A er invertibel for a ≠ 4.

Brugbart svar (0)

Svar #5
28. februar 2022 af Soeffi

#0.

$\\ \begin{pmatrix} 1 & 2 & -3 & 0\\ 1 & -2 & 2 & a\\ 5 & 5 & -3 & 0 \\ -3 & -1 & a & 0\\ \end{pmatrix} \overrightarrow{_{R_2-R_1}} \begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 5 & a\\ 5 & 5 & -3 & 0 \\ -3 & -1 & a & 0\\ \end{pmatrix}\overrightarrow{_{R_3-5R_1}} \begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 5 & a\\ 0 & -5 & 12 & 0 \\ -3 & -1 & a & 0\\ \end{pmatrix}\overrightarrow{_{R_4-3R_1}}$

$\\ \begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 5 & a\\ 0 & -5 & 12 & 0 \\ 0 & 5 & a-9 & 0\\ \end{pmatrix}\overrightarrow{_{R_4+R_3}} \begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 5 & a\\ 0 & -5 & 12 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}\overset{a\neq -3}{\overrightarrow{_{R_3-(12/(a+3))R_4}}}\begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 5 & a\\ 0 & -5 & 0 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}$

$\\ \overset{a\neq -3}{\overrightarrow{_{R_2-(5/(a+3))R_4}}}\begin{pmatrix} 1 & 2 & -3 & 0\\ 0 & -4 & 0 & a\\ 0 & -5 & 0 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}\overset{a\neq -3}{\overrightarrow{_{R_1+(3/(a+3))R_4}}}\begin{pmatrix} 1 & 2 & 0 & 0\\ 0 & -4 & 0 & a\\ 0 & -5 & 0 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}\overrightarrow{_{R_2-(4/5)R_3}}$

$\\ \begin{pmatrix} 1 & 2 & 0 & 0\\ 0 & 0 & 0 & a\\ 0 & -5 & 0 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}\overrightarrow{_{R_1+(2/5)R_3}} \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & a\\ 0 & -5 & 0 & 0 \\ 0 & 0 & a+3 & 0\\ \end{pmatrix}$

Ved to rækkeombytninger får man:

$\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & -5 & 0 & 0\\ 0 & 0 & a+3 & 0 \\ 0 & 0 & 0 & a \\ \end{pmatrix}$

Et lige antal rækkeombytninger ændrer ikke determinanten, så man får: det(B) = -5·a·(a+3). (Tilfældet a = -3, som man så bort fra undervejs, giver - ligesom formlen - det(B) = 0, da en hel rækkes elementer er lig med 0, så formlen gælder alle a.)

det(B) = 0 ⇔ a = -3 ∨ a = 0. Dvs. B er invertibel for a ≠ -3 ∧ a ≠ 0.

Skriv et svar til: Hjælp til opgave der omhandler invertible matricer.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.