Matematik

Vektor hjælp

09. april 2022 af shieo2200 - Niveau: B-niveau

Hej allesammen, sidder fast i følgende opgave. Den er dog lidt mærkelig synes jeg selv. Nogle der kan hjælpe?

Tak på forhånd, se vedhæftet fil.

Vedhæftet fil: opg 3 start.png

Svar #1
09. april 2022 af shieo2200

dette er opgaverne:

Vedhæftet fil:opg 3 midt.png

Svar #2
09. april 2022 af shieo2200

Min vinkel er hermed 45,8 grader

Svar #3
09. april 2022 af shieo2200

nogle der kan fortælle mig formler jeg skal bruge?

Brugbart svar (1)

Svar #4
09. april 2022 af SuneChr

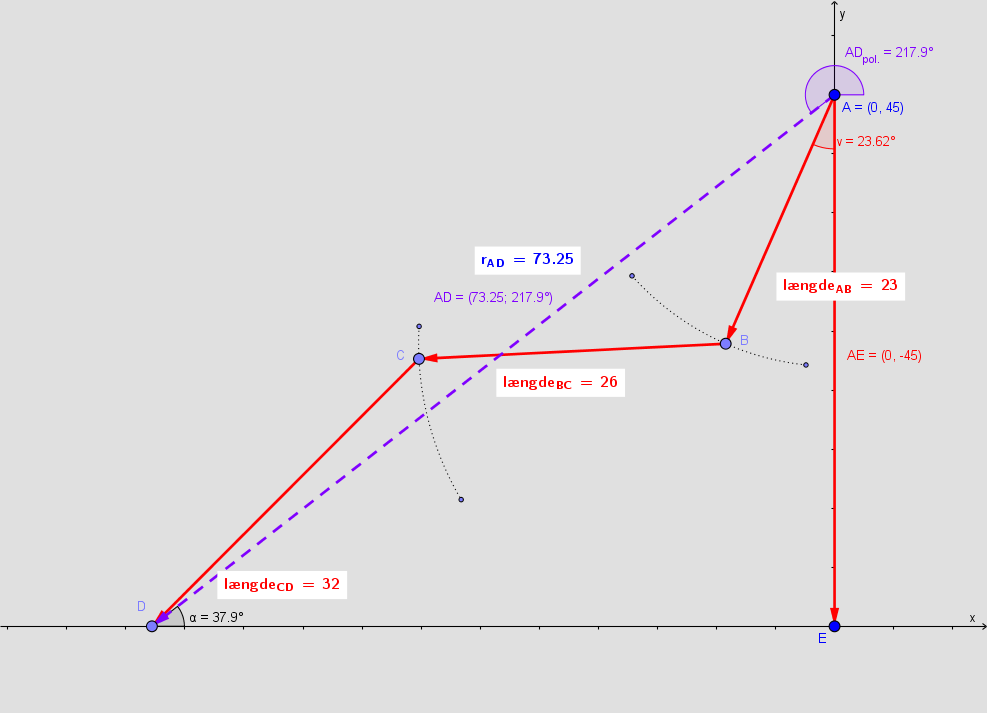
a) Vi skal angivelig ikke finde vinkel v men koordinaterne til $\overrightarrow{\textup{AB}}$
Lad den lodrette akse være x-aksens orientering og den vandrette y-akse med orientering mod venstre.
A = (45 , 0) $\overrightarrow{\textup{AB}}=\binom{-23\cos v}{23\sin v}$ $\overrightarrow{\textup{OB}}=\overrightarrow{\textup{OA}}+\overrightarrow{\textup{AB}}=\binom{45}{0}+\binom{-23\cos v}{23\sin v}$
B har samme koordinater som $\overrightarrow{\textup{OB}}$ da vektoren er stedvektor.

Brugbart svar (0)

Svar #5
09. april 2022 af ringstedLC

Opgave 1a: Din vinkel v = 45.8º virker noget stor i forhold til Figur 3.

Vedhæft gerne den opgave!

Brugbart svar (0)

Svar #6
09. april 2022 af ringstedLC

Brugbart svar (0)

Svar #7
09. april 2022 af ringstedLC

$\begin{align*} \cos(v) &= \frac{\left | \overrightarrow{AB}\cdot \overrightarrow{OA} \right |}{\left |\overrightarrow{AB} \right |\left |\overrightarrow{OA} \right |} \\ &= \frac{\left | AB_a\cdot 0+AB_b\cdot 45\right |}{23\cdot 45} \\ \left |AB_b\right | &= \frac{\cos(v)\cdot 23\cdot 45}{45} \Rightarrow \left\{\begin{matrix} AB_b=23\cdot \cos(v)\\ -AB_b=23\cdot \cos(v)\end{matrix}\right. \\ AB_b &= - 23\cdot \cos(v)\;,\;AB_b<0 \\\\ {AB_a}^2+{AB_b}^2 &= 23^2 \\ \left |AB_a \right | &= \sqrt{23^2-{AB_b}^2}\Rightarrow \left\{\begin{matrix} AB_a=\sqrt{23^2-{AB_b}^2}\\ -AB_a=\sqrt{23^2-{AB_b}^2}\end{matrix}\right. \\ AB_a &= -\sqrt{23^2-{AB_b}^2}\;,\;AB_a<0 \\ \overrightarrow{AB} &=\binom{...}{...} \end{align*}$

Brugbart svar (0)

Svar #8
09. april 2022 af ringstedLC

$\begin{align*} \overrightarrow{AD} &= \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD} \\ \overrightarrow{AD} &= \binom{r}{\theta }=\begin{pmatrix} \left | \overrightarrow{AD} \right |\\ \angle \alpha +180^{\circ}\end{pmatrix} =\begin{pmatrix} \sqrt{\bigl(x_D-x_A\bigr)^2+\bigl(y_D-y_A\bigr)^2}\\ \tan^{-1}\left (\frac{y_A\,-\,y_D}{x_A\,-\,x_D} \right )+180^{\circ} \end{pmatrix} \end{align*}$

Brugbart svar (0)

Svar #9
09. april 2022 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #10
09. april 2022 af ringstedLC

e) Lav lineær regress. på data. Bemærk om R² ≈ 1

$\begin{align*} T(t)=100 &= ...\Rightarrow t=\;?\,\textup{sek.} \end{align*}$

Svar #11
09. april 2022 af shieo2200

forstår ikke lige helt c´eren

Svar #12
09. april 2022 af shieo2200

Hvordan kan man beregne de andre vektor altså bc og cd?

Brugbart svar (0)

Svar #13
09. april 2022 af ringstedLC

#12: Du har selv bestemt vektorerne i b).

Svar #14
11. april 2022 af shieo2200

hvordan laver jeg f?

Brugbart svar (0)

Svar #15
11. april 2022 af Sofia0294

forstår heller ikke i e hvordan det giver mening at lave linære regression? hvordan kan den undersøge om forventningen er rimelig ?

Brugbart svar (1)

Svar #16
11. april 2022 af ringstedLC

#14: Regressionsudtrykket sættes lig "100", hvor sovsen koger.

Brugbart svar (0)

Svar #17
11. april 2022 af Sofia0294

men i opgaven ved man jo ikke om sovs koger på 100 grader?

Brugbart svar (0)

Svar #18
11. april 2022 af Sofia0294

kan det passe min Regressionsudtrykket er omkring y=0,292x?

Brugbart svar (1)

Svar #19
11. april 2022 af ringstedLC

#15: Opvarmningsdata til 84º er kendt (8 stk.). De ligger på, - eller tæt på den rette linje som regressionen giver. Dens R² siger noget om hvor tæt.

Brugbart svar (1)

Svar #20
11. april 2022 af ringstedLC

#17: Strengt taget har du ret. Men hvis du regner med, at sovsen hovedsaligt består af vand, så er kogepunktet 100º C.

#18:

$\begin{align*} y &= 0.254x+8.108\;,\;R^2=0.9965\quad\textup{m. GeoGebra} \\ T(t)=100 &= 0.254t+8.108 \\ t &=361.78\approx 6\,\textup{min.} \end{align*}$

Forrige 1 2 Næste

Der er 36 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.