Matematik

Areal af figur

29. juni 2022 af shain - Niveau: 9. klasse

Hvad er arealet af figuren? Kan jeg lave en hjælpe linje så jeg får 3 trekanter?

Vedhæftet fil: Screenshot_20220629-165553_Adobe Acrobat.jpg

Brugbart svar (0)

Svar #1
29. juni 2022 af mathon

Brugbart svar (0)

Svar #2
29. juni 2022 af mathon

Summen af to ens, retvinklede trekanter og et rektangel.

Svar #3
29. juni 2022 af shain

Areal rektangel: 9,6 m * 9,6 m = 92,16 m2
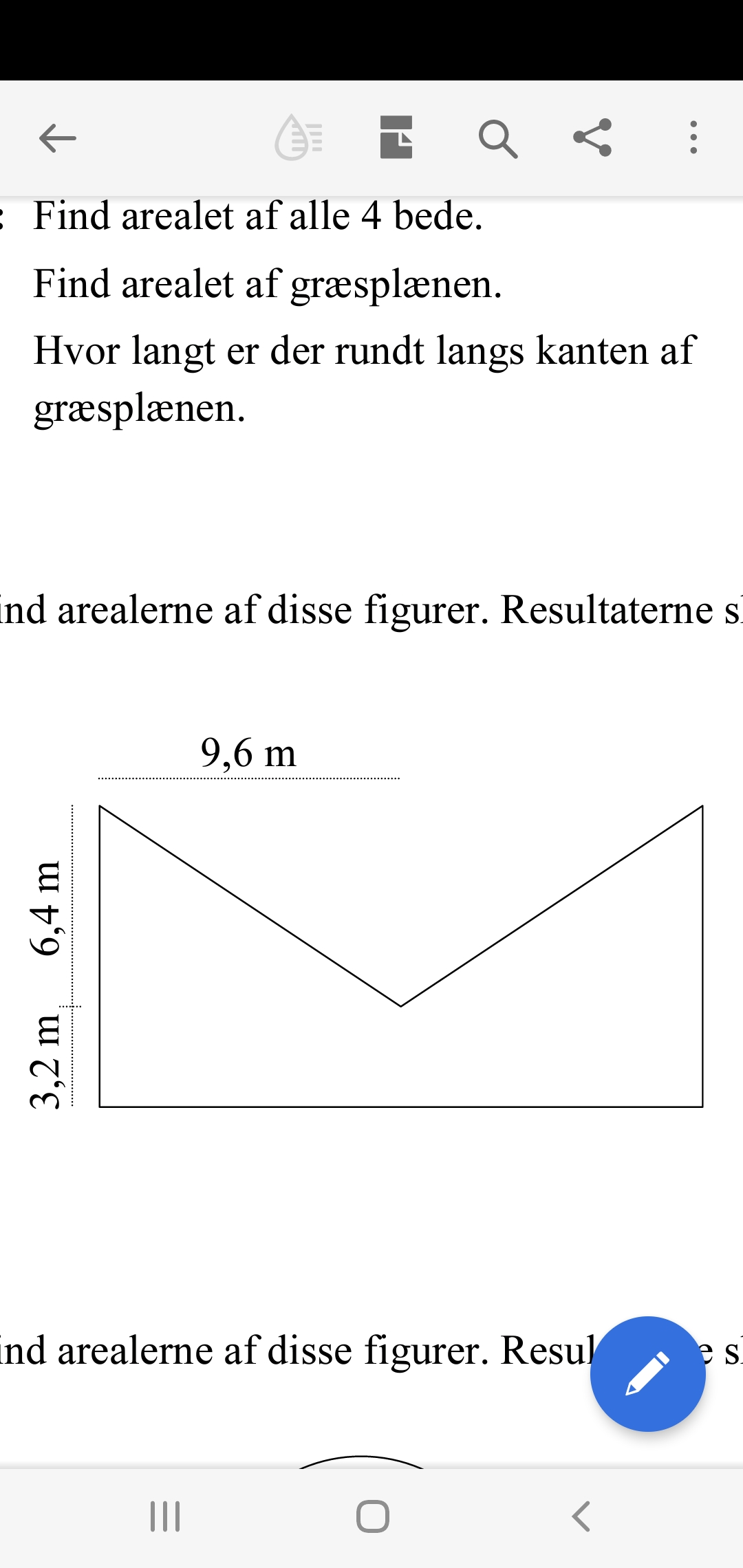
Areal trekant: (9,6 m*9,6m)/2= 46
46,06 m2 Der er trekanter skal jegcsp gange med 2?

Brugbart svar (0)

Svar #4
29. juni 2022 af ringstedLC

#0 Kan jeg lave en hjælpe linje så jeg får 3 trekanter?

Nej. Enten:

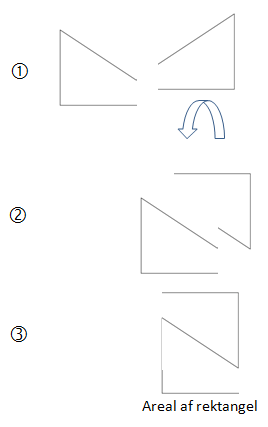
Lav en hjælpelinje, der er parallel med grundlinjen og skærer den stumpe vinkel. Så har du to ens, retvinklede trekanter med kendt grundlinje og højde, og du har ét rektangel med kendte sider. Læg de tre figurer sammen.

Eller: Lav en hjælpelinje, der skærer de to spidse vinkler. Så har du et (stort) rektangel med kendte sider og en stumpvinklet trekant. Nedfæld højden fra den stumpe vinkel på hjælpelinjen og beregn trekantens areal. Træk det fra arealet af rektanglet

#3
Areal trekant: (9,6 m*9,6m)/2= 46

er ikke trekantens areal.
.

Brugbart svar (0)

Svar #5
29. juni 2022 af mathon

$\small \small \begin{array}{llllll} \textup{Areal af:}\\&\textup{Smalt rektangel:}&& \left ( 3.2\;\mathrm{m} \right )\cdot \left ( 2\cdot \left ( 9.6\;\mathrm{m} \right ) \right )&=&61.44\;\mathrm{m^2}\\\\& 2\textup{ retvinklede trekanter:}&&2\cdot \left ( \frac{1}{2}\cdot \left ( 9.6\;\mathrm{m} \right )\cdot \left ( 6.4\;\mathrm{m} \right ) \right )&=&\underline{61.44\;\mathrm{m^2}}\\\\&\textup{Figurareal:}&&&=&122.88\;\mathrm{m^2} \end{array}$

Brugbart svar (2)

Svar #6
29. juni 2022 af SuneChr

. SP 290620222028.PNG

Vedhæftet fil:SP 290620222028.PNG

Svar #7
29. juni 2022 af shain

Er det sådan at jeg har 2 retvinklet trekanter og et smal rektangel. Hvad er højden af trekanten?

Vedhæftet fil:Screenshot_20220629-214918_WhatsApp.jpg

Brugbart svar (0)

Svar #8
29. juni 2022 af ringstedLC

De to mål tv. på figuren giver kun mening fordi delemærket flugter med den stumpe vinkel. Dét giver højden.

Brugbart svar (0)

Svar #9
30. juni 2022 af mathon

Tegn en hjælpelinje gennem det laveste punkt inde i figuren vinkelret på figurens sider.

Brugbart svar (0)

Svar #10
30. juni 2022 af mathon

I en retviklet trekant med kateterne $\small k_1\textup{ og }k_2$
er arealet:
$\small \frac{1}{2}\cdot k_1\cdot k_2$

Svar #11
30. juni 2022 af shain

billede

Vedhæftet fil:Screenshot_20220630-101106_WhatsApp.jpg

Svar #12
30. juni 2022 af shain

Hvordan bruger jeg eksempel 2, hvor jeg nedfælder højden fra den stumpe vinkel til hjælpe linjen? Areal af trekant: (19,2*6,4)/2= 61,44 m2

Skal jeg trække arealet fra rektangel areal?

Brugbart svar (0)

Svar #13
30. juni 2022 af mathon

Skal jeg trække trekantarealet fra rektanglets areal? Ja.

Svar #14
30. juni 2022 af shain

Areal af rektangel 184,32 m2
184,32 m2- 61,44 m2 = 122,88 m2?

Brugbart svar (2)

Svar #15
30. juni 2022 af mathon

$\small \begin{array}{llllr}\textup{Areal af rektangel:}&&\left ( 2\cdot \left ( 9.6\;\mathrm{m} \right ) \right )\cdot \left ( \left ( 3.2\;\mathrm{m} \right )+\left ( 6.4\;\mathrm{m} \right ) \right )&=&184.32\;\mathrm{m^2}\\\\ \textup{Areal af trekant:}&&\frac{1}{2}\cdot \left ( 6.4\;\mathrm{m} \right )\cdot \left ( 2\cdot \left ( 9.6\;\mathrm{m} \right ) \right )&=&\underline{-\;61.44\;\mathrm{m^2}}\\\\ \textup{Figurareal:}&&&=&122.88\;\mathrm{m^2} \end{array}$

Svar #16
30. juni 2022 af shain

Tusind tak for din hjælp Mathon! Sætter stor pris på det.

Skriv et svar til: Areal af figur

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.