Bestem vinkel C og længden mellem CD (med hjælpemidler)

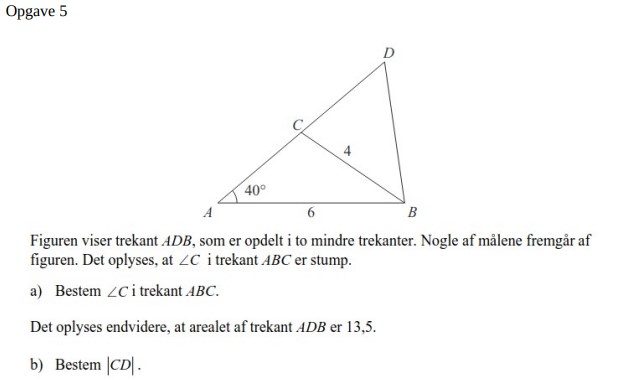
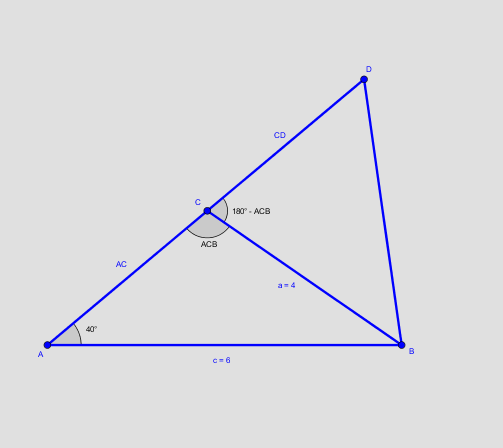
a) Brug sinusrelationerne på trekant ABC

b) Brug sinusrelationen til at finde vinkel C i ABC og dernæst kan du finde vinkel C i trekant BCD.

Nedfæld den vinkelrette fra B på AD. Kald fodpunktet for E.  trekant BCE er en retvinklet trekant, hvor du kender en vinkel og en side.

Brug dernnæst at arealet af en trekant er ½*højde*grundlinje på trekant ABD

Ad #2
Alternativ til b): Benyt (41) side 9 i din formelsamling til at bestemme AD og cos-relation til at bestemme AC.

#3: Cos-rel. bruges ved kendt vinkel og kendte vinkelben til at bestemme den modstående side eller til at bestemme en vinkel, når alle sider er kendte.

a)

b) m. sinus-rel., arealsum og "en halv ab'sin"-formel:

b) m. længdesum:

#4 
Hvorfor det, der er vel metodefrihed, når ikke andet er nævnt? cos-relationen er en ligning med fire størrelser, og når de tre er kendte, kan ligningen løses mht. den tilbageværende ubekendte (her AC).
I dette tilfælde giver det en 2.gradsligning, som kan løses med CAS. Der er to positive løsninger, men da vinkel ACB er stump, er det den mindste løsning, der er i spil. Det er forholdsvis let at argumentere for det ud fra en simpel skitse.

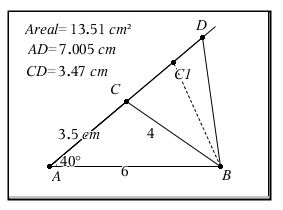
#0 En tredje metode er geometrisk løsning med D som flytbart punkt på venstre vinkelben, men dels er det lidt bøvlet at dokumentere konstruktionerne fyldestgørende og dels kan det være svært at ramme arealet af ABD på 13.5 nogenlunde nøjagtigt ved at flytte D.
Lavet i NSpire: