Matematik

Forklar og find P i koordinatsystem

03. april 2023 af Sarahmipmip - Niveau: C-niveau

Hej er der nogen der kan hjælpe mig med denne opgave:) det ville virkelig være en stor hjælp

Hvis der nogle der sidder inde med en god metode eller bare gode ideer må de rigtig gerne skrive. Opgaven er vedhæftet i skærmbilledet:)

- Sarah

Vedhæftet fil: Skærmbillede 2023-04-03 kl. 20.18.04.png

Brugbart svar (0)

Svar #1
03. april 2023 af peter lind

Brugbart svar (0)

Svar #2
03. april 2023 af peter lind

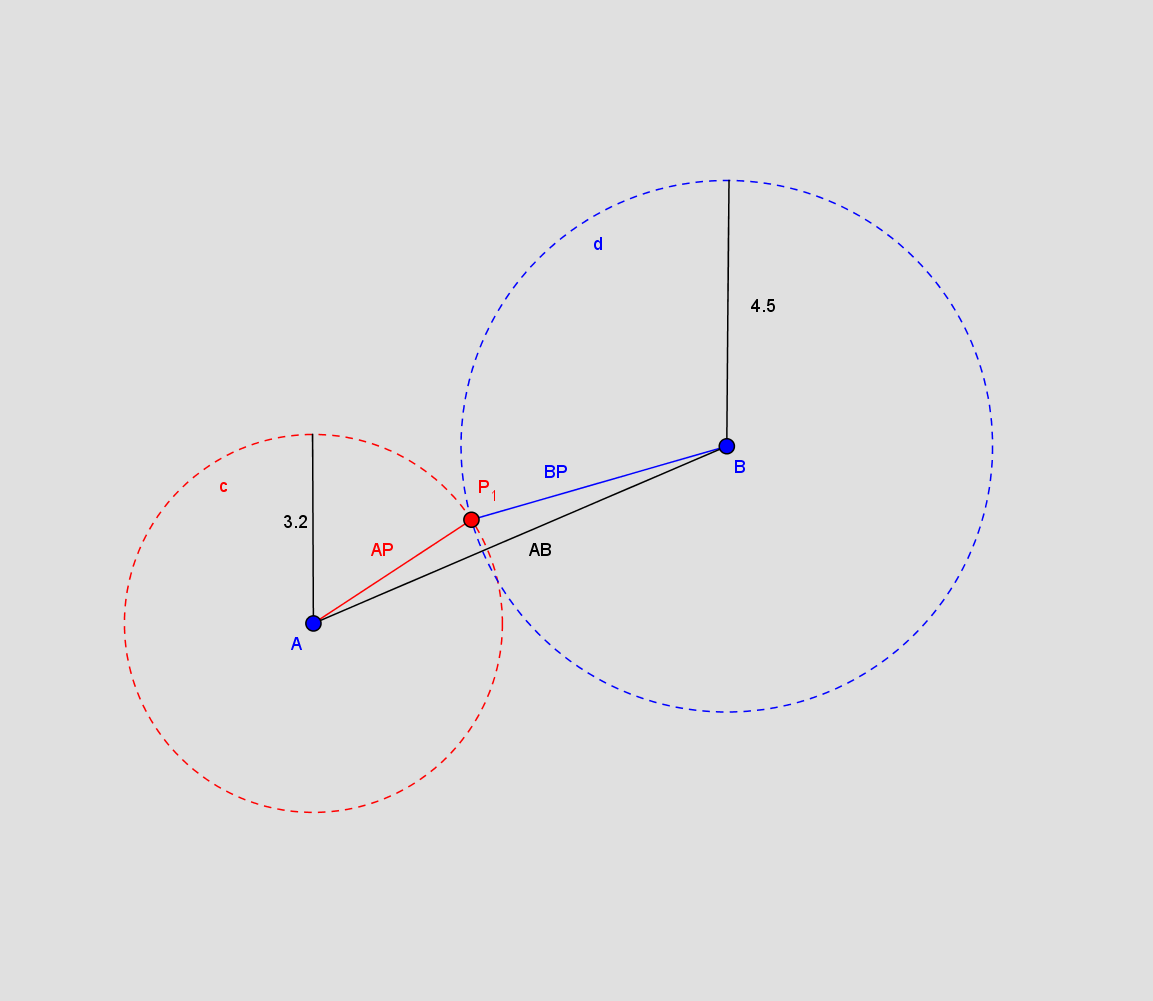
Find ligningerne for cirkler med centrum A og radius 3,2 samt cirkel med centrum B og radius 4,5

Da punkterne ligger på begge cirkler kan disse findes ved at løse ligningerne.

Brug CAS værktøj eller træk de to ligninger fra hinanden, Derved får du i stedet en lineær ligning

Svar #3
04. april 2023 af Sarahmipmip

Okay tak for hjælpen:) men jeg forstår stadig ikke opgave a. Hvad er grunden til at der findes 2 gyldige placeringer?

Brugbart svar (0)

Svar #4
04. april 2023 af jl9

Prøv og tegn 2 cirkler som skærer hinanden

Svar #5
04. april 2023 af Sarahmipmip

Det har jeg gjort i det vedhæftede skærmbillede men hvordan skal jeg forklarer det?

Vedhæftet fil:Skærmbillede 2023-04-04 kl. 12.05.40.png

Brugbart svar (0)

Svar #6
04. april 2023 af ringstedLC

#5: Radius i dine cirkler er ikke rigtige.

Indtast radius (afstanden) i kommandoen: Cirkel( <Punkt>, <radius> )

istedet for at "trække" i et punkt.

Brugbart svar (0)

Svar #7
04. april 2023 af ringstedLC

Afstanden mellem A og B er mindre end summen af afstandene AP og BP:

$\begin{align*} \textup{To sk\ae ringer kr\ae ver}:\\ |AB| &<|AP|+|BP| \\ |AB|^2 &<\Bigl(|AP|+|BP|\Bigr)^2 \\ (x_B-x_A)^2+(y_B-y_A)^2 &< \Bigl(|AP|+|BP|\Bigr)^2 \\ \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} &< |AP|+|BP| \\\\ \textup{En sk\ae ring kr\ae ver}:\\ |AB| &=|AP|+|BP| \\\\ \textup{Ingen sk\ae ringer kr\ae ver}:\\ |AB| &>|AP|+|BP|\end{align*}$

Svar #8
04. april 2023 af Sarahmipmip

er dettte rigitgt så?

Vedhæftet fil:Skærmbillede 2023-04-04 kl. 15.07.02.png

Brugbart svar (0)

Svar #9
04. april 2023 af ringstedLC

Ja.

Med kommandoen:

P: Skæring( <objekt>, <objekt> )

dannes og døbes alle skæringspunkter samtidigt.

Svar #10
05. april 2023 af Sarahmipmip

okay mange tak for hjælpen:) men hvordan skal jeg kunne forklare det? i opgave a?

Brugbart svar (0)

Svar #11
05. april 2023 af StoreNord

"Punktet P skal ligge både på en cirkel med A som centrum og på en cirkel med B som centrum.
Det gør P kun, hvis det ligger i et skæringspunkt mellem de to cirkler.
Og dem er der to af."

Brugbart svar (0)

Svar #12
05. april 2023 af StoreNord

Er læreren tilfreds med en Geogebraløsning tilspørgsmål b?

Svar #13
05. april 2023 af Sarahmipmip

Tak:) ja men hun vil også gerne have den som beregning:) har du en metode til det?

Brugbart svar (0)

Svar #14
05. april 2023 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #15
05. april 2023 af ringstedLC

#10: De to cirkler har to skæringer, da:

$\begin{align*} \bigl|AB \bigr|\; &< \bigl|AP \bigr|+\bigl|BP \bigr| && \wedge\quad \bigl|AB \bigr| > \Bigl|\bigl|AP \bigr|-\bigl|BP \bigr| \Bigr| \end{align*}$

Det vil sige, at AB er kortere end summen af de to afstande og længere end deres dfifferens.

Den første betingelse: Hvis AB var længere end af summen ville B ligge så langt fra A, at periferierne ikke havde nogle skæringer og P derfor ingen gyldige placeringer.

Den sidste betingelse: Hvis AB var kortere end differensen ville B ligge så nær A, at periferierne heller ikke havde nogle skæringer.

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #16
05. april 2023 af ringstedLC

#13: Indsæt de kendte størrelser i uligheden for to skæringer i #7 (sidste linje) og se, at den er opfyldt.

Brugbart svar (0)

Svar #17
05. april 2023 af ringstedLC

#16 rettelse:

Indsæt de kendte størrelser i nedenstående ulighed for to skæringer (næstsidste linje) og vis, at den opfyldes.

#7 rettelse:

$\begin{align*} \textup{To sk\ae ringer kr\ae ver}:\\ \bigl|AB \bigr| &< \bigl|AP \bigr|+\bigl|BP \bigr| && \wedge\ \bigl|AB \bigr| > \Bigl|\bigl|AP \bigr|-\bigl|BP \bigr| \Bigr| \\ \bigl|AB \bigr| &< r_1+r_2 && \wedge\ \bigl|AB \bigr| > \bigl|r_1-r_2\bigr| \\ \sqrt{\bigl(x_B-x_A\bigr)^2+\bigl(y_B-y_A\bigr)^2} &< r_1+r_2 \\ \Rightarrow\quad \bigl|r_1-r_2 \bigr| &< \bigl|AB \bigr| < r_1+r_2 \\\\ \textup{Ingen sk\ae ringer kr\ae ver}:\\ \bigl|AB \bigr| &> \bigl|AP \bigr|+\bigl|BP \bigr| &&\vee\ \bigl|AB \bigr| < \Bigl|\bigl|AP \bigr|-\bigl|BP \bigr| \Bigr| \\ \bigl|AB \bigr| &> r_1+r_2 &&\vee\ \bigl|AB \bigr| < \bigl|r_1-r_2\bigr| \\ \Rightarrow\quad r_1+r_2 &< \bigl|AB \bigr| < \bigl|r_1-r_2\bigr| \end{align*}$

Skriv et svar til: Forklar og find P i koordinatsystem

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.